3 Autoapprentissage compositionnel

On peut lier les données compositionnelles avec une ou plusieurs autres à l’aide de régressions linéaires, polynomiales, sinusoïdales, exponentielle, sigmoïdales, etc. Encore faut-il s’assurer que ces formes préétablies représentent le phénomène de manière fiable. Lorsque la forme de la réponse est difficile à envisager, en particulier dans des cas non-linéaires ou impliquant plusieurs variables, on pourra faire appel à des modèles dont la structure n’est pas contrôlée par une équation rigide gouvernée par des paramètres (comme la pente ou l’intercept). L’autoapprentissage vise à détecter des structures complexes émergeant d’ensembles de données à l’aide des mathématiques et de processus automatisés afin de prédire l’émergence de futures occurrences.

3.1 Lexique

L’autoapprentissage possède son jargon particulier. Les variables réponse sont celles que nous comptons prédire, alors que les variables d’entrée sont utilisées pour prédire une réponse. Alors que l’apprentissage supervisé inclue une variable réponse, l’apprentissage non-supervisé, lui, n’en a pas: il est surtout utilisé pour créer des catégories à partir de données qui ne sont pas préalablement étiquettées. Les apprentissages par régression prédisent des variables continuent alors que les apprentissage par classification prédisent des catégories. Les données d’entraînement servent à ajuster le modèle alors que les données de test servent à évaluer sa performance.

3.2 Démarche

3.2.1 Prétraitement

Pour la plupart des techniques d’autoapprentissage, le choix de l’échelle de mesure est déterminant sur la modélisation subséquente. Par exemple, un algorithme basé sur la distance comme les k plus proches voisins ne mesurera pas les mêmes distances entre deux observations si l’on change l’unité de mesure d’une variable du mètre au kilomètre. En outre, les transformations compositionnelles sont une forme de prétraitement.

3.2.2 Entraînement et test

Un modèle prut fonctionner très bien en terrain connu, mais une prédiction doit être évaluée sur des données pour lesquelles le modèle ne connait pas la réponse. En pratique, il faut séparer un tableau de données en deux: un tableau d’entraînement et un tableau de test. Il n’existe pas de standards sur la proportion à utiliser dans l’un et l’autre. Rarement, toutefois, réservera-t-on moins plus de 50% et moins de 20% à la phase de test. Dans tous les cas, on doit porter une attention particulière à l’équilibre des données dans chaque tableau (les distributions devraient être semblables). L’analyste doit s’assurer de séparer le tableau au hasard pour ne pas biaiser le modèle, mais de manière consciencieuse pour éviter d’évacuer des cas rares dans un tableau ou dans l’autre.

3.2.3 Validation croisée

Lorsque l’on considère une structure comme du bruit, on est dans un cas de sousapprentissage. Lorsque, au contraire, on interprète du bruit comme une structure, on est en cas de surapprentissage. Une manière de limiter le mésapprentissage est d’avoir recours à la validation croisée. La validation croisée est un principe incluant plusieurs algorithmes qui consiste à entraîner le modèle sur un échantillonnage aléatoire des données d’entraînement. La technique la plus utilisée est le k-fold, où l’on sépare aléatoirement le tableau d’entraînement en un nombre k de tableaux. À chaque étape de la validation croisée, on calibre le modèle sur tous les tableaux sauf un, puis on valide le modèle sur le tableau exclu.

3.2.4 Choix de l’algorithme d’apprentissage

Choisir l’algorithme (ou les algorithmes) adéquats pour votre problème n’est pas une tâche facile. Ce choix sera motivé par le problème à régler, les tenants et aboutissants des algorithmes, votre expérience, l’expérience de la littérature, l’expérience de vos collègues, etc. Ce serait peu productif d’étudier la mathématique de chacun d’eux. Une approche raisonnable est de tester plusieurs modèles, de retenir les modèles qui semblent les plus pertinents, et d’approfondir si ce n’est déjà fait la mathématique des options retenues et d’apprendre à les maîtriser au fil de vos expériences. Le module scikit-learn, qui fonctionne en langage Python, propose néanmoins un schéma décisionnel.

Schéma décisionnel des algorithmes pertinents. Source: [scikit-learn](https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html).

Figure 3.1: Schéma décisionnel des algorithmes pertinents. Source: scikit-learn.

3.2.5 Déploiement

Nous ne couvrirons pas la phase de déploiement d’un modèle. Notons seulement qu’il est possible, en R, d’exporter un modèle dans un fichier .Rdata, qui pourra être chargé dans un autre environnement R. Cet environnement peut être une feuille de calcul comme une interface visuelle montée par exemple avec Shiny.

3.3 En résumé,

Explorer les données
Sélectionner des algorithmes
Effectuer un prétraitement
Créer un ensemble d’entraînement et un ensemble de test
Lisser les données sur les données d’entraînement avec validation croisée
Tester le modèle
Déployer le modèle

3.4 L’autoapprentissage en R

Plusieurs options sont disponibles. Je vais introduire le module caret de R a été conçu pour donner accès à des centaines de fonctions d’autoapprentissage via une interface commune.

library("tidyverse")
library("compositions")
library("caret")

Pour cet atelier, nous allons couvrir les k plus proches voisins et les processus gaussiens.

3.5 Les k plus proches voisins

Le principe des KNN (k-nearest neighbors: un objet va ressembler à ce qui se trouve dans son voisinage.

Les KNN se basent en effet sur une métrique de distance pour rechercher un nombre k de points situés à proximité de la mesure. Les k points les plus proches sont retenus, k étant un entier non nul à optimiser. Un autre paramètre parfois utilisé est la distance maximale des voisins à considérer: un voisin trop éloigné pourra être discarté. La réponse attribuée à la mesure est calculée à partir de la réponse des k voisins retenus. Dans le cas d’une régression, on utiliser généralement la moyenne. Dans le cas de la classification, la mesure prendra la catégorie qui sera la plus présente chez les k plus proches voisins. La métrique de distance devient importante et une standardisation des données (par exemple soustraire la moyenne, puis diviser par l’écart-type) est généralement nécessaire en prétraitement. Pour ce qui est des données compositionnelles, on pourra tirer profit de la métrique d’Aitchison en calculant les distances euclidienne sur des données transformées par clr ou ilr.

3.5.1 Exemple d’application

L’ionome foliaire est la concentration en éléments d’une feuille: ce sont des données compositionnelles. Nous allons prédire une espèce fictive à partir de son ionome seulement (si d’autres variables étaient intégrées à la prédiction, il faudrait standardiser les données).

veggies <- read_csv("data/legumes_fictifs.csv")
head(veggies)

## # A tibble: 6 x 7
##   Culture   Annee     N     P     K    Ca    Mg
##   <chr>     <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 PanetRave  2007  3.13  0.36  5.33  1.96  0.36
## 2 PanetRave  2007  3.03  0.37  4.94  2.33  0.4 
## 3 PanetRave  2007  3.01  0.36  5.08  1.76  0.36
## 4 PanetRave  2007  3.53  0.36  5.44  2.13  0.37
## 5 PanetRave  2007  3.96  0.38  6.1   2.76  0.5 
## 6 PanetRave  2007  3.9   0.38  6.06  2.66  0.48

Effectuons un prétraitement compositionnel sous forme d’ilr.

veggies <- veggies %>%
  mutate(Fv = 100 - (N+P+K+Ca+Mg))
sbp <- matrix(c(1, 1, 1, 1, 1,-1,
                1, 1,-1,-1,-1, 0,
                1,-1, 0, 0, 0, 0,
                0, 0, 1,-1,-1, 0,
                0, 0, 0, 1,-1, 0), ncol = 6, byrow = TRUE)
veggies_ilr <- veggies %>%
  dplyr::select(N, P, K, Ca, Mg, Fv) %>%
  ilr(., V = gsi.buildilrBase(t(sbp))) %>%
  as_tibble() %>%
  mutate(Culture = veggies$Culture)

Séparons les données en entraînement (_tr) et en test (_te) en utilisant la fonction caret::createDataPartition avec une proportion 70/30 (p = 0.7). Il est essentiel d’utiliser set.seed() pour s’assurer que la partition soit la même à chaque session de code (pour la reproductibilité) - j’ai l’habitude de taper n’importe quel numéro à environ 6 chiffres, mais lors de publications, je vais sur random.org et je génère un numéro au hasard, sans biais.

set.seed(68017)
id_tr <- createDataPartition(veggies_ilr$Culture, p = 0.7, list = FALSE)
veggies_tr <- veggies_ilr[id_tr, ]
veggies_te <- veggies_ilr[-id_tr, ]

L’objet id_tr comprend les indices de ligne des données d’entraînement. Avant de lancer nos calculs, allons vois sur la page de caret les modules qui effectuent des KNN pour la classification. Nous trouvons knn et kknn. Prenons kknn. Nous pourrions utiliser une grille de paramètre pour l’optimisation du modèle, mais laissons caret générer une grille par défaut. Nous allons néamoins modéliser avec une validation croisée à 5 plis.

ctrl <- trainControl(method="repeatedcv", repeats = 5)

Pour finalement lisser le modèle.

set.seed(8961704)
clf <- train(Culture ~ .,
             data = veggies_tr,
             method = "kknn",
             trainControl = ctrl)
clf

## k-Nearest Neighbors 
## 
## 342 samples
##   5 predictor
##   4 classes: 'ChouMarseille', 'Courgine', 'PanetRave', 'PommeMer' 
## 
## No pre-processing
## Resampling: Bootstrapped (25 reps) 
## Summary of sample sizes: 342, 342, 342, 342, 342, 342, ... 
## Resampling results across tuning parameters:
## 
##   kmax  Accuracy   Kappa    
##   5     0.9738582  0.9647107
##   7     0.9738582  0.9647107
##   9     0.9738582  0.9647107
## 
## Tuning parameter 'distance' was held constant at a value of 2
## 
## Tuning parameter 'kernel' was held constant at a value of optimal
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were kmax = 9, distance = 2 and
##  kernel = optimal.

Nous obtenons les paramètres du modèle optimal. Prédisons l’espèce selon son ionome pour chacun des tableaux.

pred_tr <- predict(clf)
pred_te <- predict(clf, newdata = veggies_te)

Une manière d’évaluer la prédiction est d’afficher un tableau de contingence.

table(Observed = veggies_tr$Culture, Predicted = pred_tr)

##                Predicted
## Observed        ChouMarseille Courgine PanetRave PommeMer
##   ChouMarseille            67        0         0        0
##   Courgine                  0       95         0        0
##   PanetRave                 0        0       101        0
##   PommeMer                  0        0         0       79

table(Observed = veggies_te$Culture, Predicted = pred_te)

##                Predicted
## Observed        ChouMarseille Courgine PanetRave PommeMer
##   ChouMarseille            27        0         1        0
##   Courgine                  0       40         0        0
##   PanetRave                 3        0        39        0
##   PommeMer                  0        0         0       33

Les espèces sont toutes classées en entraînement, mais quelques rares erreurs surviennent en test. Pas mal comme classement!

3.6 Les processus gaussiens

Les prédictions que nous avons obtenues des KNN sont des catégories, mais on aurait pu aussi prédire des nombres réels. Dans les cas où la crédibilité de la réponse est importante, il devient pertinent que la sortie soit probabiliste: les prédictions seront alors présentées sous forme de distributions de probabilité. Les processus gaussiens snt en mesure de prédire des distributions (prédictions probabilistes).

Le principe des processus gaussiens (gaussian processes, GP) est de générer une distribution multinormale (comprenant théoriquement une infinité de dimensions) à l’aide d’une matrice de covariance qui doit être définie (que l’on nomme le noyau) et d’un vecteur de moyenne (normalement composés de zéros pour une variable-réponse centrée), puis d’en sortir une distribution a posteriori conditionnée sur les observations. Les GP sont semblables à la modélisation de la variance courrament utilisée en géostatistiques. Pour plus de détails, référez-vous aux notes du cours Anayse et modélisation d’agroécosystèmes. Pour l’instant, retenez que (1) la matrice de covariance a une influence capitale et que (2) vous devez préférablement standardiser (centrer et réduire) vos entrées et nécessairement vos réponses.

3.6.1 Exemple d’application

Les données de pollution en métaux lourds sur une rive de la rivière Meuse, en France, sont souvent utilisées pour les exemples d’application en prédiction spatiale. Nous allons utiliser les processus gaussiens (avec le module kernlab) pour prédire les ilr des métaux lourds à partir des coordonnées et de la distance de la rivière, en profitant de l’occasion pour cartographier avec les modules ggmap et sf. Notez que les ilr sont ici les variables-réponse, alors qu’ils étaient les variables d’entrée dans l’exemple précédent avec les KNN.

library("ggmap")
library("sf")
meuse <- read_csv("data/meuse.csv")
meuse %>% head()

## # A tibble: 6 x 14
##        x      y cadmium copper  lead  zinc  elev    dist    om ffreq  soil
##    <dbl>  <dbl>   <dbl>  <dbl> <dbl> <dbl> <dbl>   <dbl> <dbl> <dbl> <dbl>
## 1 181072 333611    11.7     85   299  1022  7.91 0.00136  13.6     1     1
## 2 181025 333558     8.6     81   277  1141  6.98 0.0122   14       1     1
## 3 181165 333537     6.5     68   199   640  7.8  0.103    13       1     1
## 4 181298 333484     2.6     81   116   257  7.66 0.190     8       1     2
## 5 181307 333330     2.8     48   117   269  7.48 0.277     8.7     1     2
## 6 181390 333260     3       61   137   281  7.79 0.364     7.8     1     2
## # ... with 3 more variables: lime <dbl>, landuse <chr>, dist.m <dbl>

Les coordonnées sont exprimées en format néerlandais EPSG:28992. Transformons-les en longitudes et latitudes sur l’ellipsoïde NAD83 avec le module sf.

meuse_geo <- meuse %>%
  st_as_sf(coords = c("x", "y"), crs = 28992) %>%
  st_transform("+proj=longlat +datum=NAD83")
meuse_coord <- meuse_geo %>%
  st_coordinates() %>%
  as_tibble() %>%
  mutate(cadmium = meuse$cadmium,
         copper = meuse$copper,
         lead = meuse$lead,
         zinc = meuse$zinc,
         dist = meuse$dist) %>%
  rename(x = "X", y = "Y")
meuse_coord %>% head()

## # A tibble: 6 x 7
##       x     y cadmium copper  lead  zinc    dist
##   <dbl> <dbl>   <dbl>  <dbl> <dbl> <dbl>   <dbl>
## 1  5.76  51.0    11.7     85   299  1022 0.00136
## 2  5.76  51.0     8.6     81   277  1141 0.0122 
## 3  5.76  51.0     6.5     68   199   640 0.103  
## 4  5.76  51.0     2.6     81   116   257 0.190  
## 5  5.76  51.0     2.8     48   117   269 0.277  
## 6  5.76  51.0     3       61   137   281 0.364

À partir des coordonnées, nous pouvons grâce à ggmap::get_stamenmap effectuer une requête pour télécherger les tuiles d’un fond de carte, sur lesquels nous affichons nous concentrations en zinc.

meuse_map <- get_stamenmap(bbox = c(left = 5.716, right = 5.767, bottom = 50.95, top = 51),
                           zoom = 14, maptype = "terrain")
ggmap(meuse_map) +
  geom_point(data = meuse_coord, aes(x=x, y=y, fill = zinc), shape = 21, size = 2) +
  scale_fill_viridis_c(option = "inferno", direction = -1) +
  theme_bw()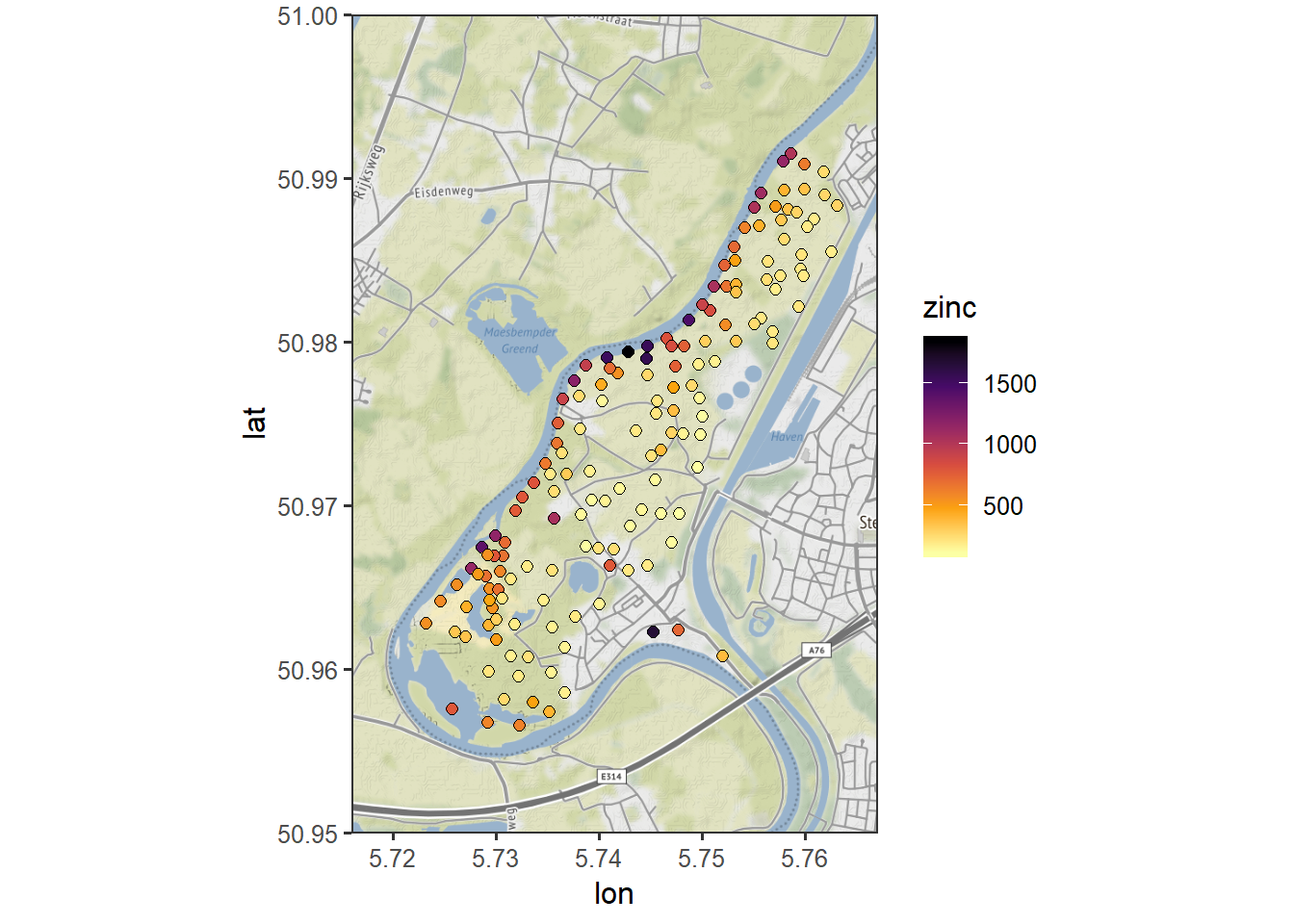

Figure 3.2: Mesures de concentration en zinc dans les sols d’une rive de la rivière Meuse

Transformons maintenant nos concentrations en ilr.

sbp <- matrix(c(1, 1, 1, 1,-1,
                1, 1,-1,-1, 0,
                1,-1, 0, 0, 0,
                0, 0, 1,-1, 0),
              ncol = 5, byrow = TRUE)
psi <- gsi.buildilrBase(t(sbp))

meuse_ilr <- meuse %>%
  mutate(Fv = 1e6 - cadmium - copper - lead - zinc) %>%
  dplyr::select(cadmium, copper, lead, zinc, Fv) %>%
  acomp(.) %>%
  ilr(., V = psi) %>%
  as_tibble()

names(meuse_ilr) <- c("CdCuPbZn.Fv",
                      "CdCu.PbZn",
                      "Cd.Cu",
                      "Pb.Zn")

meuse_ilr %>% head()

## # A tibble: 6 x 4
##   CdCuPbZn.Fv CdCu.PbZn Cd.Cu  Pb.Zn
##         <dbl>     <dbl> <dbl>  <dbl>
## 1       -7.99     -2.86 -1.40 -0.869
## 2       -8.06     -3.06 -1.59 -1.00 
## 3       -8.37     -2.83 -1.66 -0.826
## 4       -8.86     -2.48 -2.43 -0.562
## 5       -8.94     -2.73 -2.01 -0.589
## 6       -8.83     -2.67 -2.13 -0.508

Ces données sont jumelées avec les coordonnées et la distance de la rivière pour créer un tableau prêt pour l’autoapprentissage.

meuse_ml <- meuse_coord %>%
  dplyr::select(x, y, dist) %>%
  bind_cols(meuse_ilr)

Puis, séparons les données.

set.seed(1046584)
train_id <- createDataPartition(meuse$y, p=0.7, list=FALSE)# #pour obtenir un équilibre sur les latitudes
meuse_tr <- meuse_ml[train_id, ]
meuse_te <- meuse_ml[-train_id, ]

Bien que l’autoapprentissage sera effectué avec caret, vous aurez avantage à prendre davantage de contrôle sur les processus gaussiens en utilisant directement la fonction kernlab::gausspr(), qui permettra du coup de prédire l’incertitude de la prédiction. Notez toutefois que R ne possède toujours pas de module polyvalent pour les processus gaussiens, ce qui me motive habituellement à basculer en Python à cette étape. Continuons néanmoins avec R, en sélectionnant un noyau de type radial que nous ne tenterons pas d’optimiser et sur lesquels nous laissons tomber la validation croisée pour éviter de compliquer l’exemple. Enfin, notez les données sont dans ce cas-ci mises automatiquement à l’échelle.

set.seed(4896378)
mod_CdCuPbZn.Fv <- train(CdCuPbZn.Fv ~ x + y + dist,
                         data = meuse_tr,
                         method = "knn")
mod_CdCu.PbZn <- train(CdCu.PbZn ~ x + y + dist,
                         data = meuse_tr,
                         method = "gaussprRadial")
mod_Cd.Cu <- train(Cd.Cu ~ x + y + dist,
                         data = meuse_tr,
                         method = "gaussprRadial")
mod_Pb.Zn<- train(Pb.Zn ~ x + y + dist,
                         data = meuse_tr,
                         method = "gaussprRadial")

Effectuons la série de prédictions en remettant le tout dans l’échelle originale.

pred1_tr <- predict(mod_CdCuPbZn.Fv)
pred1_te <- predict(mod_CdCuPbZn.Fv, newdata = meuse_te)
pred2_tr <- predict(mod_CdCu.PbZn)
pred2_te <- predict(mod_CdCu.PbZn, newdata = meuse_te)
pred3_tr <- predict(mod_Cd.Cu)
pred3_te <- predict(mod_Cd.Cu, newdata = meuse_te)
pred4_tr <- predict(mod_Pb.Zn)
pred4_te <- predict(mod_Pb.Zn, newdata = meuse_te)

Nous pouvons évaluer notre modèle en comparant les prédictions.

par(mfrow = c(4, 2))
plot(meuse_tr$CdCuPbZn.Fv, pred1_tr, main = "Train") ; abline(0, 1, col="red")
plot(meuse_te$CdCuPbZn.Fv, pred1_te, main = "Test") ; abline(0, 1, col="red")
plot(meuse_tr$CdCu.PbZn, pred2_tr, main = "Train") ; abline(0, 1, col="red")
plot(meuse_te$CdCu.PbZn, pred2_te, main = "Test") ; abline(0, 1, col="red")
plot(meuse_tr$Cd.Cu, pred3_tr, main = "Train") ; abline(0, 1, col="red")
plot(meuse_te$Cd.Cu, pred3_te, main = "Test") ; abline(0, 1, col="red")
plot(meuse_tr$Pb.Zn, pred4_tr, main = "Train") ; abline(0, 1, col="red")
plot(meuse_te$Pb.Zn, pred4_te, main = "Test") ; abline(0, 1, col="red")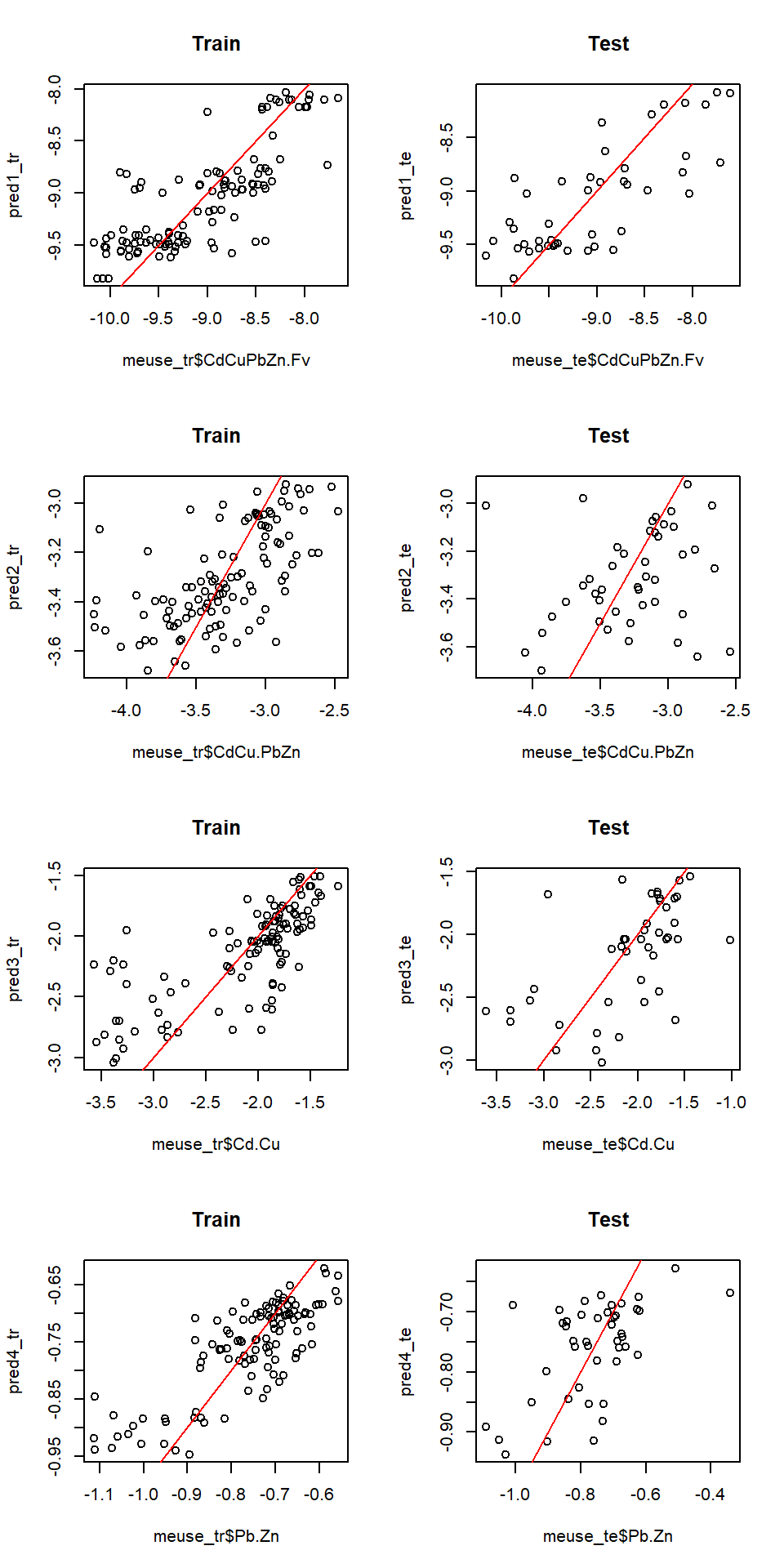

Figure 3.3: Évaluation visuelle de la prédiction spatiale par processus gaussien

Les résultats montrent que les modèles ne sont pas exceptionnels, et qu’une optimisation critique et conscientieuse devrait être effectuée en vue d’obtenir de meilleures prédictions. Continuons néanmoins.

La prédiction spatiale demande une grille comprenant des points sur lesquels on voudra effectuer des prédictions. Il est possible d’en créer une de différentes manières en R ou dans des systèmes d’information géographique. Dans ce cas, elle est disponible en format csv.

meuse_grid <-  read_csv("data/meuse_grid.csv")
meuse_grid %>% head()

## # A tibble: 6 x 7
##        x      y part.a part.b   dist  soil ffreq
##    <dbl>  <dbl>  <dbl>  <dbl>  <dbl> <dbl> <dbl>
## 1 181180 333740      1      0 0          1     1
## 2 181140 333700      1      0 0          1     1
## 3 181180 333700      1      0 0.0122     1     1
## 4 181220 333700      1      0 0.0435     1     1
## 5 181100 333660      1      0 0          1     1
## 6 181140 333660      1      0 0.0122     1     1

meuse_grid %>%
  ggplot(aes(x=x, y=y)) +
  coord_fixed() +
  geom_point(size=0.1) +
  theme_bw()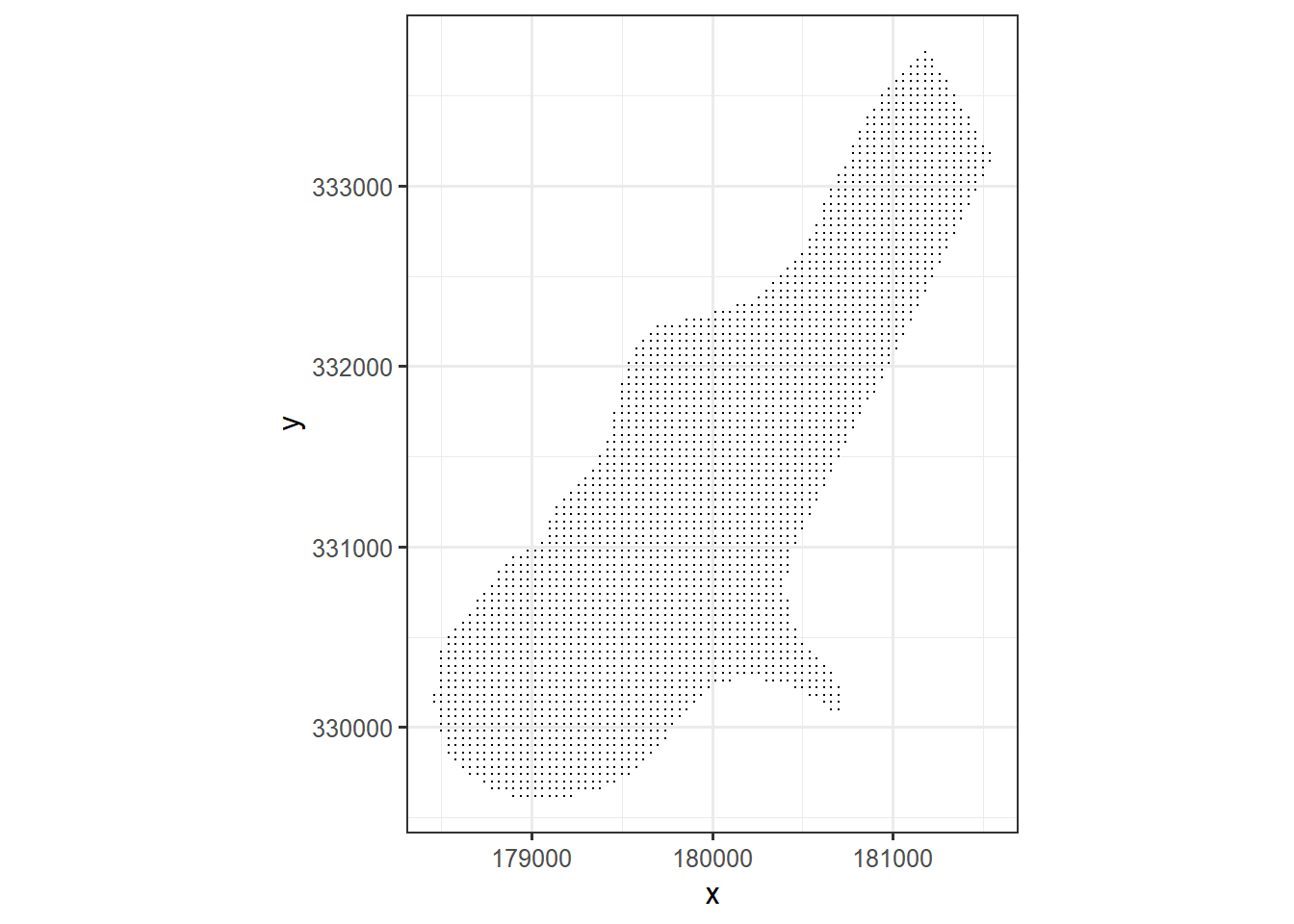

Figure 3.4: Grille pour la prédiction spatiale.

Ramenons les coordonnées sur une même référence que celles utilisées pour la prédiction.

meuse_grid_coord <- meuse_grid %>%
  st_as_sf(coords = c("x", "y"), crs = 28992) %>%
  st_transform("+proj=longlat +datum=NAD83") %>%
  st_coordinates() %>%
  as_tibble() %>%
  mutate(dist = meuse_grid$dist) %>%
  rename(x = "X", y = "Y")

Effectuons les prédictions des ilr sur la grille.

pred1 <- predict(mod_CdCuPbZn.Fv, newdata = meuse_grid_coord)
pred2 <- predict(mod_CdCu.PbZn, newdata = meuse_grid_coord)
pred3 <- predict(mod_Cd.Cu, newdata = meuse_grid_coord)
pred4 <- predict(mod_Pb.Zn, newdata = meuse_grid_coord)

Ces prédictions sont consignées dans un tableau.

meuse_pred <- meuse_grid_coord %>%
  as_tibble() %>%
  mutate(CdCuPbZn.Fv = pred1,
         CdCu.PbZn = pred2,
         Cd.Cu = pred3,
         Pb.Zn = pred4)

Ce tableau est utiliser pour effectuer la transformation inverse de l’ilr à la composition.

# Transformation inverse
meuse_pred_comp <- meuse_pred %>%
  dplyr::select(CdCuPbZn.Fv, CdCu.PbZn, Cd.Cu, Pb.Zn) %>%
  ilrInv(., V=psi)

# En ppm
meuse_pred_comp <- unclass(meuse_pred_comp) * 1e6

# En format tibble avec les bons noms
meuse_pred_comp <- meuse_pred_comp %>%
  as_tibble() %>%
  rename("cadmium" = "V1",
         "copper" = "V2",
         "lead" = "V3",
         "zinc" = "V4",
         "Fv" = "V5")

## Warning: `as_tibble.matrix()` requires a matrix with column names or a `.name_repair` argument. Using compatibility `.name_repair`.
## This warning is displayed once per session.

# Fusionner avec le tableau de prédiction
meuse_pred_comp <- bind_cols(meuse_pred, meuse_pred_comp)

Enfin, nous pouvons projeter les résultats sur notre carte pour chaque point de la grille.

gg_cd <- ggmap(meuse_map) +
  geom_point(data = meuse_pred_comp, aes(x=x, y=y, colour = cadmium)) +
  geom_point(data = meuse_coord, aes(x=x, y=y, size = cadmium), shape = 1) +
  scale_colour_viridis_c(option = "inferno", direction = -1) +
  theme_bw()
gg_cu <- ggmap(meuse_map) +
  geom_point(data = meuse_pred_comp, aes(x=x, y=y, colour = copper)) +
  geom_point(data = meuse_coord, aes(x=x, y=y, size = copper), shape = 1) +
  scale_colour_viridis_c(option = "inferno", direction = -1) +
  theme_bw()
gg_pb <- ggmap(meuse_map) +
  geom_point(data = meuse_pred_comp, aes(x=x, y=y, colour = lead)) +
  geom_point(data = meuse_coord, aes(x=x, y=y, size = lead), shape = 1) +
  scale_colour_viridis_c(option = "inferno", direction = -1) +
  theme_bw()
gg_zn <- ggmap(meuse_map) +
  geom_point(data = meuse_pred_comp, aes(x=x, y=y, colour = zinc)) +
  geom_point(data = meuse_coord, aes(x=x, y=y, size = zinc), shape = 1) +
  scale_colour_viridis_c(option = "inferno", direction = -1) +
  theme_bw()

cowplot::plot_grid(gg_cd, gg_cu, gg_pb, gg_zn, ncol = 2)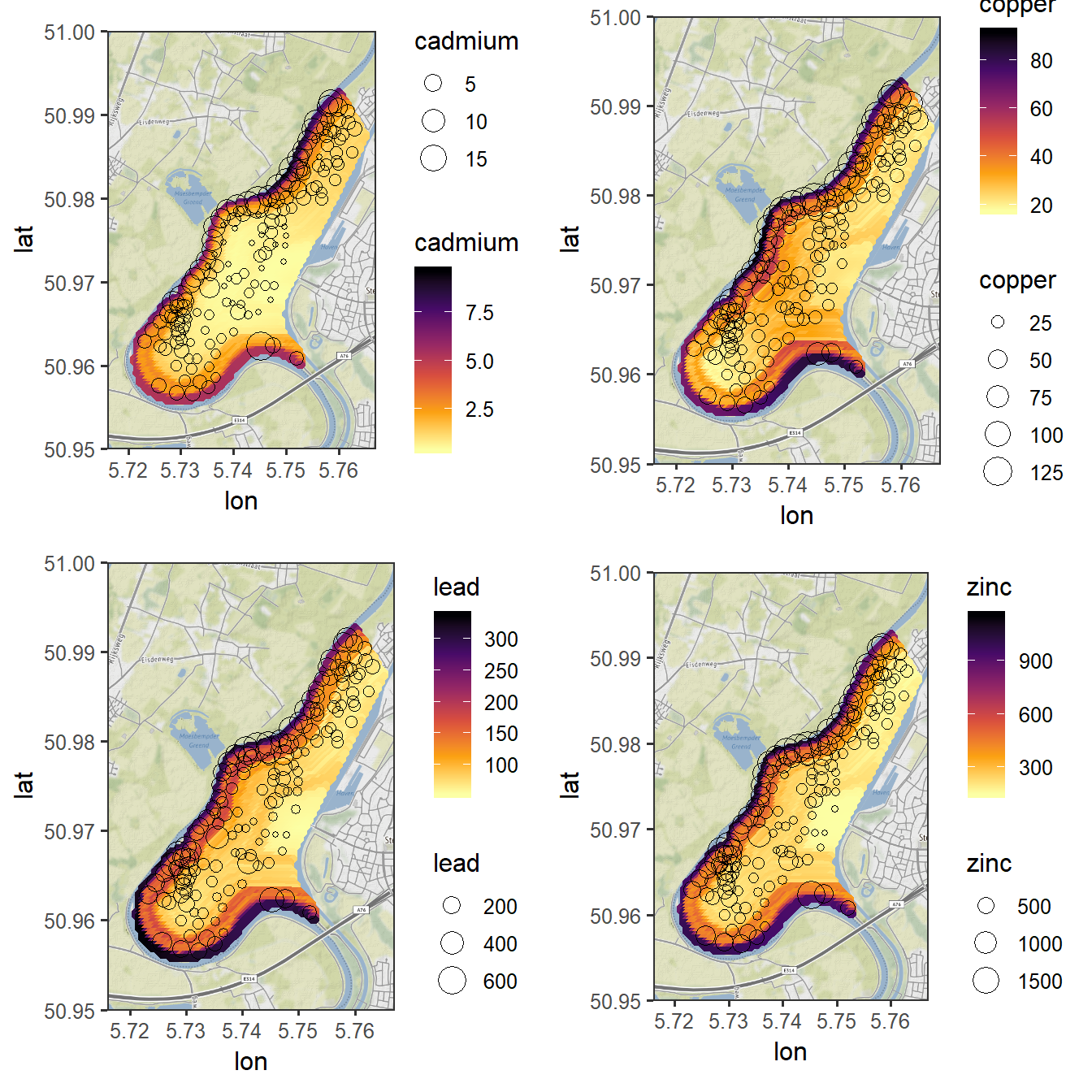

Figure 3.5: Prédiction spatiale des métaux lourds sur une rive de la rivière Meuse.

Tu as raison, Bugs. Ça suffit pour aujourd’hui.