13 Les données géospatiales
️ Objectifs spécifiques:
À la fin de ce chapitre, vous
- saurez cartographier des données géoréférencées avec ggplot
- serez en mesure d’effectuer un autoapprentissage spatial
- saurez utiliser R comme outil d’analyse spatiale (donnée associées à des points, lignes, polygones et rasters)
13.1 Les données spatiales
Des données associées à un endroit sont spatiales. Puisque ce cours ne traite pas d’écologie exoplanétaire, nous traiterons en particulier de données géospatiales, mot que l’on utilise pour désigner des données avec référence spatiale sur la planète Terre.
Lorsque nous avons abordé les séries temporelles, j’ai pris pour acquis que nous utilisions le calendrier grégorien comme référence temporelle. Les données géospatiales, quant à elles, sont souvent exprimées en termes d’angles donnant une position à la surface d’une référence dont la forme est un ellipsoide de révolution (le système géodésique): la longitude décrivant l’angle de part et d’autre (entre 0° et 180° Ouest ou Est) du méridien de référence (le premier méridien, près de Greenwich) et la latitude décrivant l’angle entre l’équateur et l’un des pôles (entre 0° et 90° Nord ou Sud). Les angles sont parfois exprimées sous forme degré° minute' seconde'' Sens cardinal, par exemple 46° 53' 21.659'' S. Toutefois, il est plus commun (et plus pratique) d’exprimer les angles de manière décimale, accompagnée d’un signe pour indiquer le sens cardinal (par convention positif au Nord et à l’Est). Par exemple, on exprimerait 46° 53' 21.659'' S sous forme décimale par les opérations suivantes.
\[ secondes = \frac{21.659''}{3600'' \cdot °^{-1}} = 0.00602° \]
\[ minutes = \frac{53'}{60' \cdot °^{-1}} = 0.883° \]
\[ - \left( 46° + 0.883° + 0.00602° \right) = -46.889° \]
La référence de l’altitude est généralement donnée par rapport à un géoïde, qui est une élévation théorique du niveau de la mer ainsi qu’une direction de la gravité évaluée sur toute la surface du globe.
Toutefois, les angles ne sont pas pratiques pour évaluer des distances, ce que l’on fera bien mieux sur une carte. Pour présenter la Terre sous forme de carte, on cré des représentations applaties du globe sous forme de carte avec l’aide d’équations de projection.
Or, il existe différents systèmes géodésiques, différents géoides et de nombreuses manières de calculer les projections. Ainsi, il est important de spécifier les références utilisées lorsque l’on donne dans la précision. Pour cette séance, je prendrai pour acquis que vous possédez certaines bases en positionnement, qui sont par ailleurs essentielles pour pratiquer adéquatement un métier scientifique.
Dans ce chapitre, j’utiliserai notamment comme exemple d’application des données météorologiques soutirées d’Environnement Canada grâce au module weathercan, obtenues entre les longitudes -60° et -80° et entre les latitudes 45° et 50° en mai 2018. J’ai effectué quelques opérations pour obtenir des indicateurs météo: degrés-jour (somme des degrés de température moyenne > 5 °C, degree_days), précipitations totales (cumul_precip) et indice de diversité des précipitations (plus l’indice sdi s’approche de 1, plus les températures sont uniformément distribuées pendant la période). Les calculs sont consignés dans le fichier lib/12_weather-fetch.R, mais étant donné que le téléchargement prend pas mal de temps, j’ai créé un csv. Les coordonnées se trouvent dans les colonnes de latitude (lat) et longitude (lon).
source("lib/12_weather-fetch.R")## # A tibble: 6 x 8
## station_id station_name prov lat lon degree_days cumul_precip sdi
## <dbl> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 10247 ILE AUX GRUES QC 47.1 -70.5 NA NA NA
## 2 10661 NORTHEAST MARGAREE (AUT) NS 46.4 -61.0 372. 222. 0.904
## 3 10732 NICOLET QC 46.2 -72.7 823. 78.4 0.704
## 4 10761 MCTAVISH QC 45.5 -73.6 915. 107 0.740
## 5 10762 STE-CLOTILDE QC 45.2 -73.7 860. 85.2 0.820
## 6 10763 ILES DE LA MADELEINE QC 47.4 -61.8 326. 167. 0.853Dans le tableau weather, chaque observation est liée à un point dans l’espace. Dans ce cas, nous avons tous les outils nécessaires pour afficher nos points dans l’espace (figure ??).
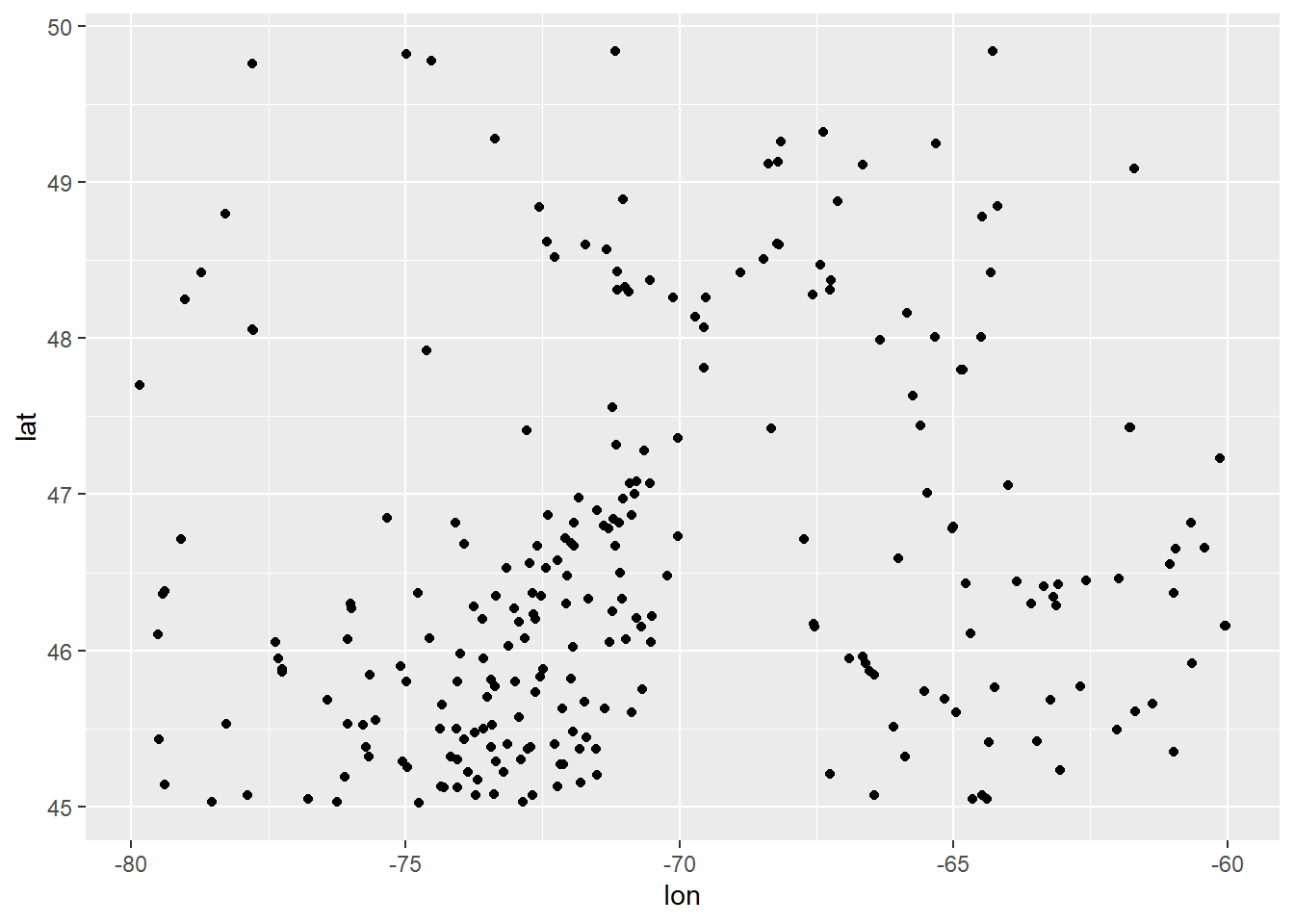
Figure 13.1: Position des stations météo du tableau weather
Si vous avez l’oeil averti, vous avez peut-être repéré le Québec, le Nouveau-Brunswick et la frontière avec les États-Unis. L’absence de repère rend néanmoins difficle l’interprétation de cette carte.
13.2 Cartographier avec le module ggmap
Le module ggmap ajoute des couches d’images téléchargées depuis des services de cartorgaphie en ligne. Dans cette section, nous allons utiliser le service de carte Stamen, qui ne demande pas de frais d’utilisation ou d’enregistrement particulier. La fonction get_stamenmap() demande une boîte de coordonnées délimitant la carte à produire, un paramètre de zoom (plus le zoom est élevé, plus la carte incluera de détails: un zoom de 2 est suffisant pour une carte du monde, mais pour l’Est du Canada, on prendra plutôt un zoom de 6 - un bon zoom est obtenu par tâtonnement) et accessoirement un type de carte.
library("ggmap")
east_canada <- get_stamenmap(bbox = c(left=-81, right = -59, bottom = 44, top = 51),
zoom = 6,
maptype = "terrain")Pour afficher la carte, nous enchâssons notre objet dans une fonction ggmap(), à laquelle nous pouvons ajouter une couche.
ggmap(east_canada) +
geom_point(data = weather, mapping = aes(x = lon, y = lat))Une approche plus généraliste consiste à spécifier dans la fonction ggmap() l’agument de base utilisé pour lancer un graphique ggplot, comme à la figure figure ??. En outre, l’utiliation de l’argument base_layer permet d’effectuer des fecettes et d’éviter de spécifier la source des données dans toutes les couches subséquentes.
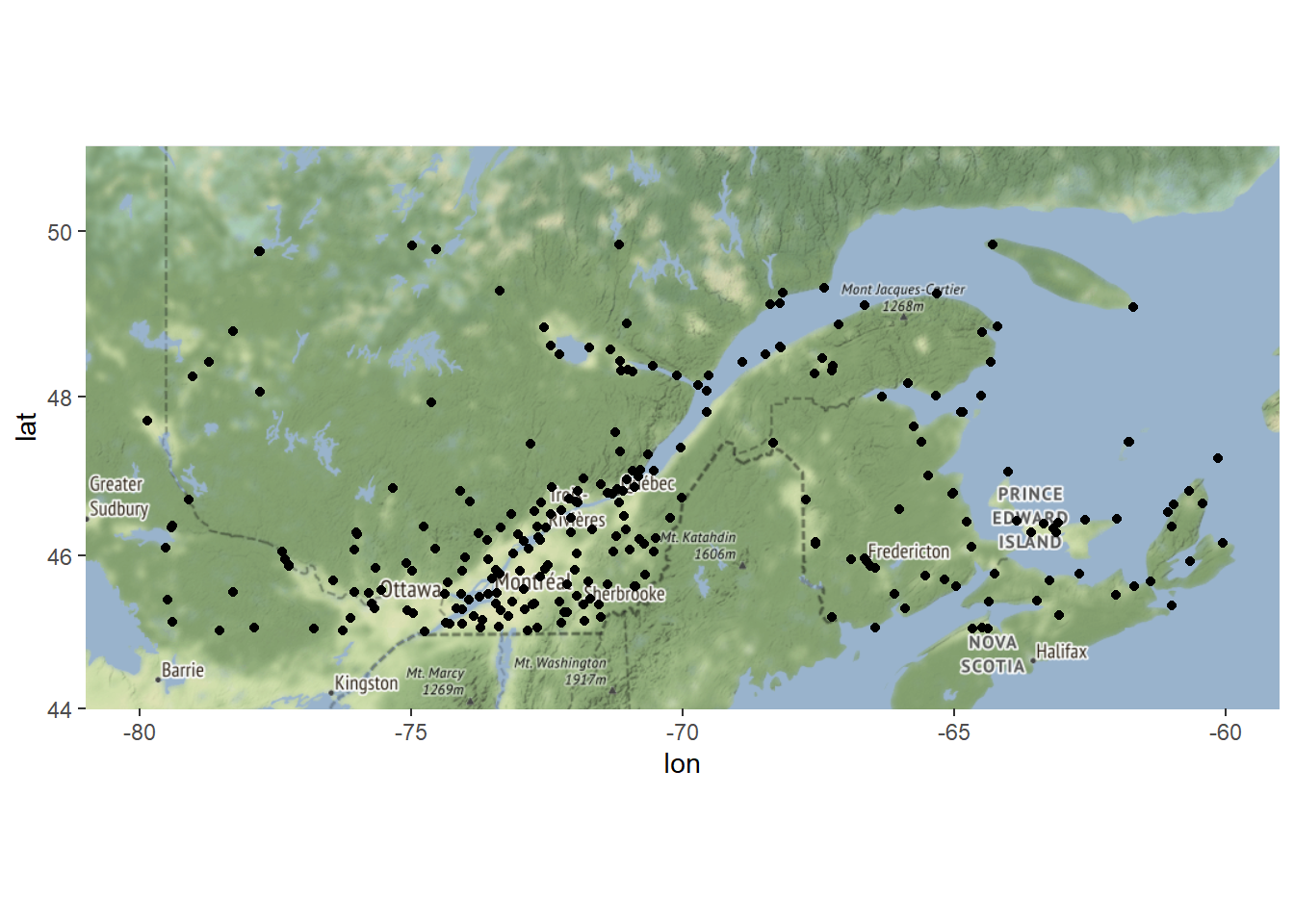
Figure 13.2: Position des stations météo du tableau weather superposé à une carte importée par ggmap
La carte que nous avons créée est de type terrain, un type d’affichage efficace mais peu approprié pour une publication visant à être imprimée. Le type toner-lite est davantage voué à l’impression, alors que le type watercolor est plus joli pour le web. Les types offerts sont listés dans la ficher d’aide ?get_stamenmap.
maptype = c("terrain", "terrain-background", "terrain-labels",
"terrain-lines", "toner", "toner-2010", "toner-2011",
"toner-background", "toner-hybrid",
"toner-labels", "toner-lines", "toner-lite", "watercolor")13.3 Types génériques de données spatiales
Nous avons jusqu’à présent utilisé des données spatiales attachées à un point. Ce ne sont pas les seuls.
- Données ponctuelles: associées à un point. Exemple: mesure à un endroit précis.
- Données linéaires: associées à une série de point. Exemple: mesure associée à une route ou une rivière.
- Données de polygone: associées à une aire délimitée par des points. Exemples: Données associées à un champ, une unité administrative, un bassin versant, etc.
- Données raster: associées à une grille. Exemple: une image satellite où chaque pixel est associé à un recouvrement foliaire.
L’enregistrement des données ponctuelles ne posent pas de défi particulier. Les données associées à un ligne, toutefois posent un problème d’organisation, puisqu’une ligne elle-même contient des informations sur les coordonnées de ses points ainsi que l’ordre dans lequel les points sont connectés. On pourra soit créer un tableau de données ayant une colonne où l’identifiant de la ligne est consigné, renvoyant à un autre tableau où chaque ligne décrit un point en terme d’identifiant de ligne à laquelle il appartient, ses coordonnées, ainsi que sont ordre de rattachement dans la ligne. Les informations de la ligne pourraient aussi être enchâssées dans une cellule de tableau de données, en tant que sous-tableau. Ou bien, on pourrait créer un tableau sous forme de jointure entre le tableau des données et le tableau des lignes. Un défi similaire pourrait subvenir avec des polygones, qui demandent davantage d’information étant donnée qu’ils peuvent être troués (par exemple un lac) ou séparés en différents morceaux (un archipel, par exemple). Enfin, il existe des formats de données spatiales génériques (shapefiles et geojson) ou spécialement conçus pour R (module sf), que nous couvrirons plus loin dans ce chapitre.
13.4 Les choroplèthe
Les cartes de type choroplèthe se présentent sous forme de polygones décrits par un groupe et un ordre, dont un la couleur de remplissage dépend d’une variable. Les pays, par exemple, forment des polygones.
## long lat group order region subregion
## 1 -69.89912 12.45200 1 1 Aruba <NA>
## 2 -69.89571 12.42300 1 2 Aruba <NA>
## 3 -69.94219 12.43853 1 3 Aruba <NA>
## 4 -70.00415 12.50049 1 4 Aruba <NA>
## 5 -70.06612 12.54697 1 5 Aruba <NA>
## 6 -70.05088 12.59707 1 6 Aruba <NA>La fonction map_data() de ggplot2 permet de soutirer des polygone de certaines cartes. Pour les zones géographiques prédéfinies, il est préférable de soutirer les polygones désirées de données existantes plutôt que les créer soi-même. Souvent, ces polygones ne sont pas directement disponibles en R. Dans ce cas, il faudra trouver des fichiers de carte auprès de Statistique Canada, Données Québec, etc., ce que nous verrons plus loin.
especes_menacees <- read_csv('data/WILD_LIFE_14012020030114795.csv')
iucn_oecd <- especes_menacees %>%
dplyr::filter(IUCN == "THREATENED", SPEC == "MAMMAL") %>%
dplyr::select(Country, Value) %>%
dplyr::group_by(Country) %>%
dplyr::summarise(n_threatened_species = sum(Value)) %>%
dplyr::arrange(desc(n_threatened_species))Les noms des pays doivent correspondre exactement, et la colonne des pays doit porter le même nom (j’ai inspecté les vecteurs iucn_oecd30$Country et unique(world$region)).
iucn_oecd <- iucn_oecd %>%
replace(.=="United States", "USA") %>%
replace(.=="Slovak Republic", "Slovakia") %>%
replace(.=="United Kingdom", "UK") %>%
dplyr::rename("region" = "Country")Les espèces sont jointes au tableau contenant les polygones.
Pour le graphique de la figure ??, La stratégie est de créer des polygones groupés par groupes de polygones (group = group), dont la couleur de remplissage correspond à au nombre d’espèce. J’ajoute coord_map() en spécifiant une projection de type Mercator (essayez projection = "ortho"). Le reste est de la décoration.
ggplot(world_iucn, aes(long, lat)) +
geom_polygon(aes(group = group, fill = n_threatened_species),
colour = "grey50", lwd = 0.1) +
coord_map(projection = "mercator", xlim = c(-180, 180), ylim = c(-90, 90)) +
scale_fill_gradient(low = "#8CBFE6", high = "#FF0099", na.value = "grey70") +
labs(title = "Number of threatened species in OECD countries",
subtitle = "Source: OCDE, 2019") +
theme(panel.background = element_rect(fill = "grey97"),
plot.background = element_rect(fill = "white"),
axis.text = element_blank(),
axis.ticks = element_blank(),
axis.title = element_blank(),
panel.grid = element_blank()) +
guides(fill = guide_legend(title = "Number of\nthreatened\nspecies"))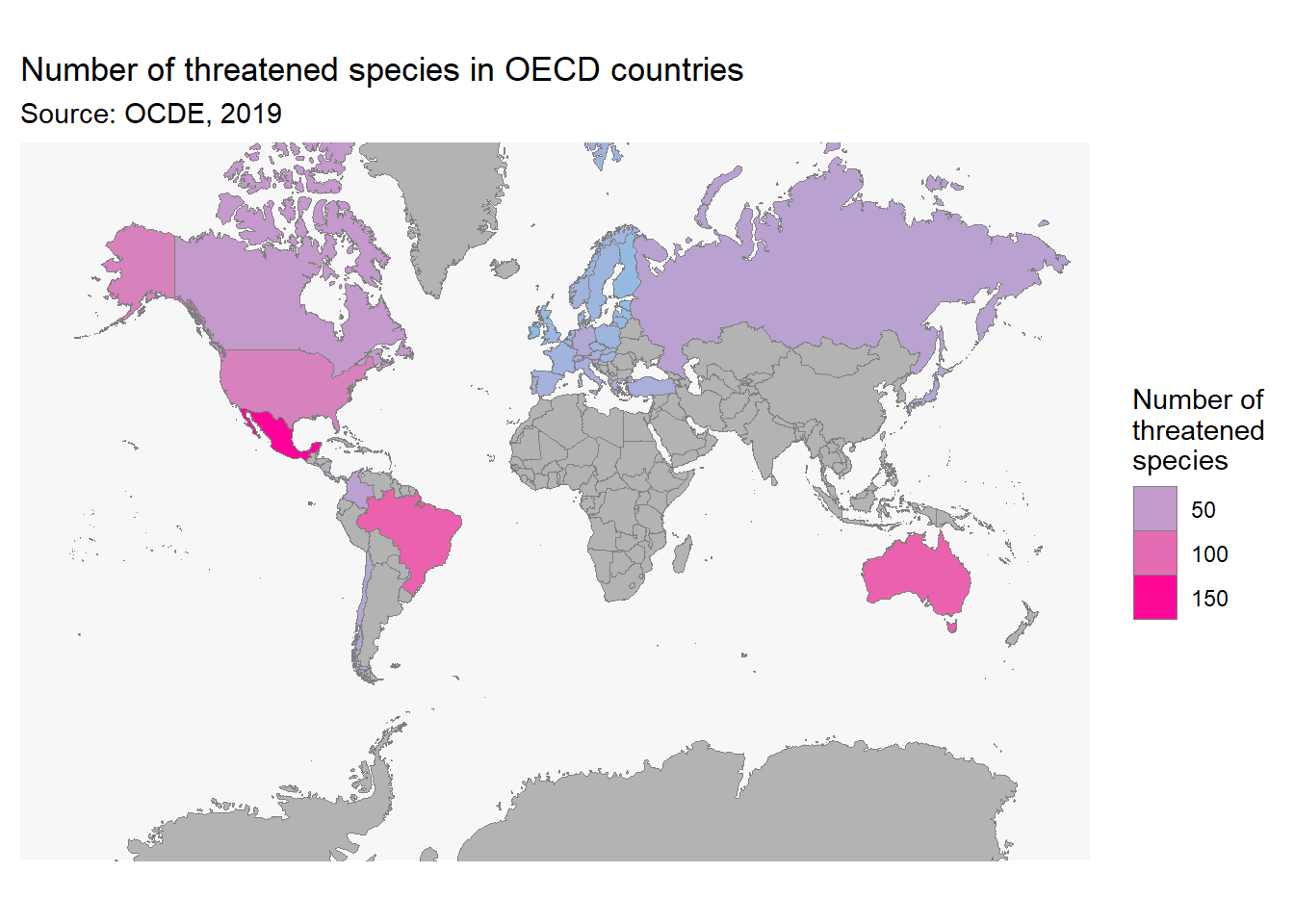
Figure 13.3: Nombre d’espèces en danger dans les pays de l’OCDE
Comme c’est le cas des points de la figure ??, on peut superposer des choroplèthes à des cartes téléchargées (figure ??).
worldmap <- get_stamenmap(bbox = c(left=-170, right = 170, bottom = -80, top = 80),
zoom = 2,
maptype = "watercolor")
world_iucn_oecd <- world_iucn %>%
filter(!is.na(n_threatened_species))
ggmap(worldmap,
base_layer = ggplot(world_iucn_oecd, aes(long, lat))) +
geom_polygon(aes(group = group, fill = n_threatened_species),
colour = "black", lwd = 0.2) +
coord_map(projection = "mercator", xlim = c(-180, 180), ylim = c(-90, 90)) +
scale_fill_gradient(low = "blue", high = "red", na.value = "grey80") +
labs(title = "Number of threatened species in OECD countries",
subtitle = "Source: OCDE, 2019") +
theme(axis.text = element_blank(),
axis.ticks = element_blank(),
axis.title = element_blank(),
panel.grid = element_blank()) +
guides(fill = guide_legend(title = "Number of\nthreatened\nspecies"))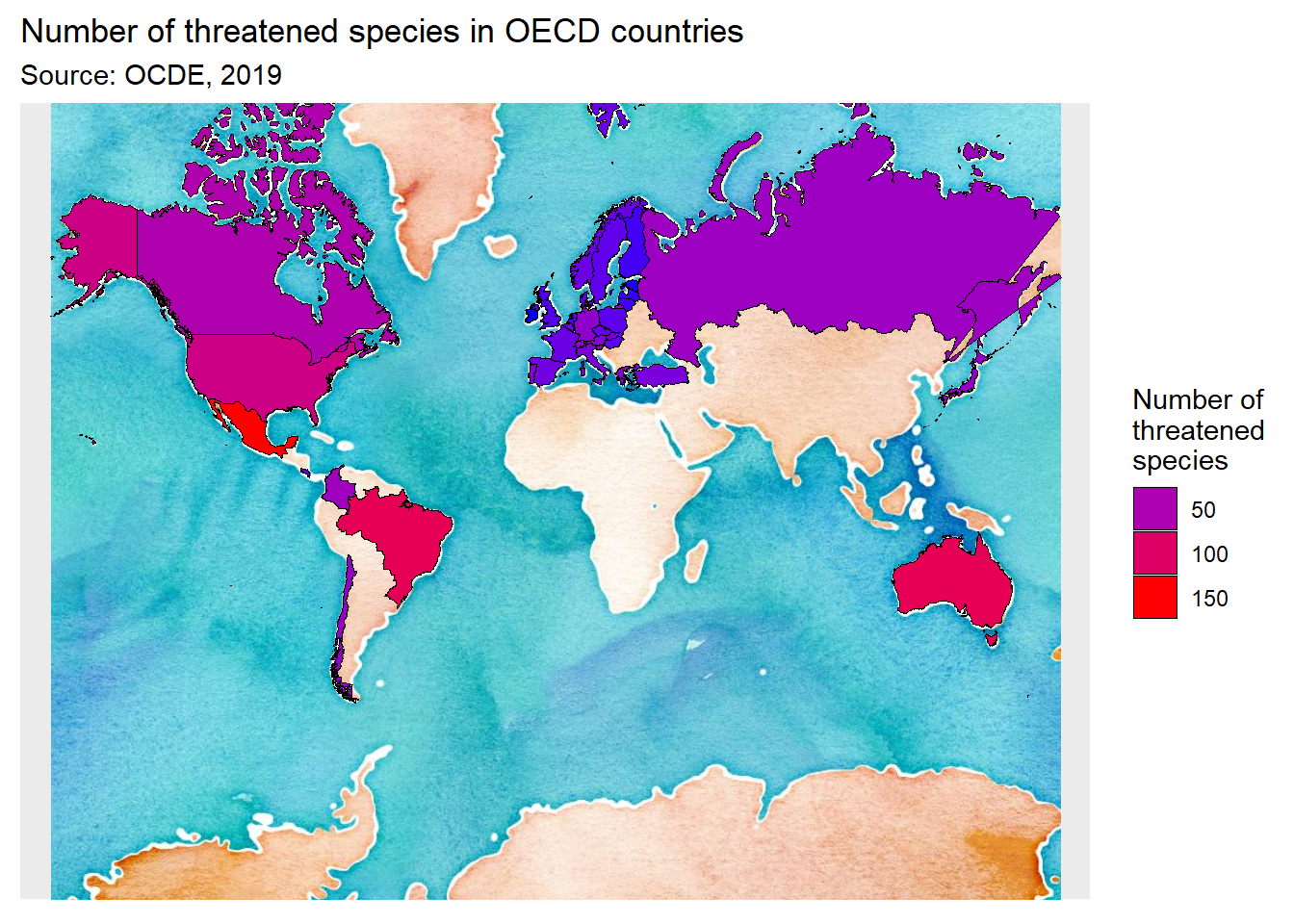
Figure 13.4: Nombre d’espèces en danger dans les pays de l’OCDE superposé à une carte importée par ggmap
Si vous savez créer des polygones, vous saurez créer des lignes de manière similaire avec la couche graphique geom_path(). Pour les rasters, c’est moins évident.
13.5 Les rasters
Les rasters sont des données associées à un grille. Nous avons introduit la fonction expand.grid() au chapitre 11 lorsque nous désirions créer un tableau où chaque ligne désigne une des combinaisons possibles d’hyperparamètres pour ajuster un modèle d’autoapprentissage. De même, nous pouvons créer une grille comprenant les combinaisons de longitudes et de latitudes, puis créer une variable spatialisée \(z = 10\times sin \left( xy \right) - 0.01x^2 + 0.05y^2\).
grid <- expand.grid(lon = seq(from = -80, to = -60, by = 0.25),
lat = seq(from = 45, to = 50, by = 0.25))
grid <- grid %>%
mutate(z = 10*sin(lon*lat) - 0.01*lon^2 + 0.05*lat^2) # créer une variable spatialisée
grid %>% head()## lon lat z
## 1 -80.00 45 39.87084
## 2 -79.75 45 28.96923
## 3 -79.50 45 31.05725
## 4 -79.25 45 43.60578
## 5 -79.00 45 48.42839
## 6 -78.75 45 38.89957Pour visualiser une grille avec ggplot2, on peut avoir recourt à la couche graphique geom_tile(), dont la couleur remplissage est associée à la colonne z du tableau. Ce type de graphique est appelée heatmap (figure ??).
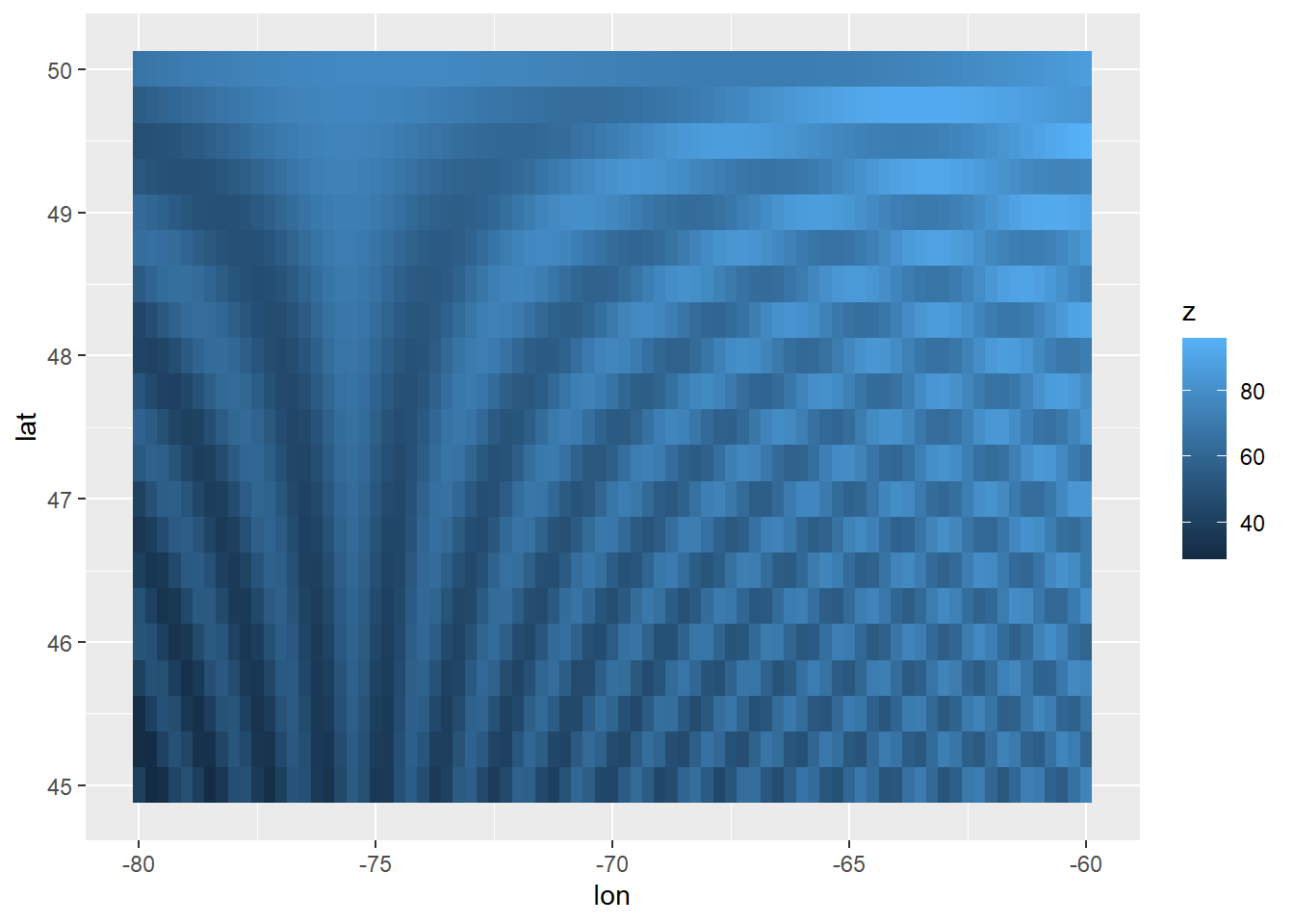
Remarquez que j’ai créé une fonction pour générer une variable spatialisée. Une telle fonction n’a pas besoin d’être inventée: on peut en créer une en utilisant les outils que nous avons appris jusqu’à présent, en particulier avec l’autoapprentissage.
13.6 Autoapprentissage spatial
La géostatistique est l’étude statistique des variables spatiales, un sujet complexe qui sort du cadre de ce cours - que vous pourrez creuser dans le livre Applied Spatial Data Analysis with R. Ici, nous allons projeter des variables spatialisées à l’aide de l’autoapprentissage, où la position (coordonnées en longitude et latitude, par exemple) peut servir de variable prédictive (ainsi que, éventuellement, des variables spatialisées concernant l’altitude, l’hydrologie, la géomorphologie, l’écologie, la sociologie, la gestion du territoire, etc.). Pour ce faire, vous pourrez utiliser algorithme qui convient à vos données et à votre domaine d’étude. Nous allons utiliser les processus gaussiens, qui sont particulièrement utiles pour évaluer l’incertitude des prédictions. Par exemple, nous allons prédire sur une grille les données de degrés-jour du tableau weather avec un processus gaussien. Pour évaluer la performance d’une prédiction, n’oublions de séparer nos données en jeux d’entraînement et de test (avec la fonction caret::createDataPartition())!
library("caret")
weather_dd <- weather %>%
dplyr::select(lon, lat, degree_days) %>%
drop_na()
weather_dd_sc <- weather_dd %>%
mutate(degree_days = (degree_days - mean(degree_days))/sd(degree_days))
train_id <- createDataPartition(
y = weather_dd_sc$degree_days,
p = 0.7,
list = FALSE
)[, 1]Utilisons la fonction kernlab::gausspr(), vue au chapitre 11.
library("kernlab")
dd_gp <- gausspr(x = weather_dd_sc[train_id, c("lon", "lat")],
y = weather_dd_sc[train_id, "degree_days"],
kernel = "rbfdot",
#kpar = list(sigma = 01), # laisser optimiser
variance.model = TRUE,
scale = TRUE,
var = 0.1,
cross = 5)## Using automatic sigma estimation (sigest) for RBF or laplace kernelÉvaluons visuellement al performance de la prédiction (figure ??).
pred_dd_tr <- predict(dd_gp)
pred_dd_te <- predict(dd_gp, newdata = weather_dd_sc[-train_id, c("lon", "lat")])
par(mfrow = c(1, 2))
plot(weather_dd_sc$degree_days[train_id], pred_dd_tr, main = "Train prediction", xlab = "mesuré", ylab = "prédit")
abline(0, 1, col="red")
plot(weather_dd_sc$degree_days[-train_id], pred_dd_te, main = "Test prediction", xlab = "mesuré", ylab = "prédit")
abline(0, 1, col="red")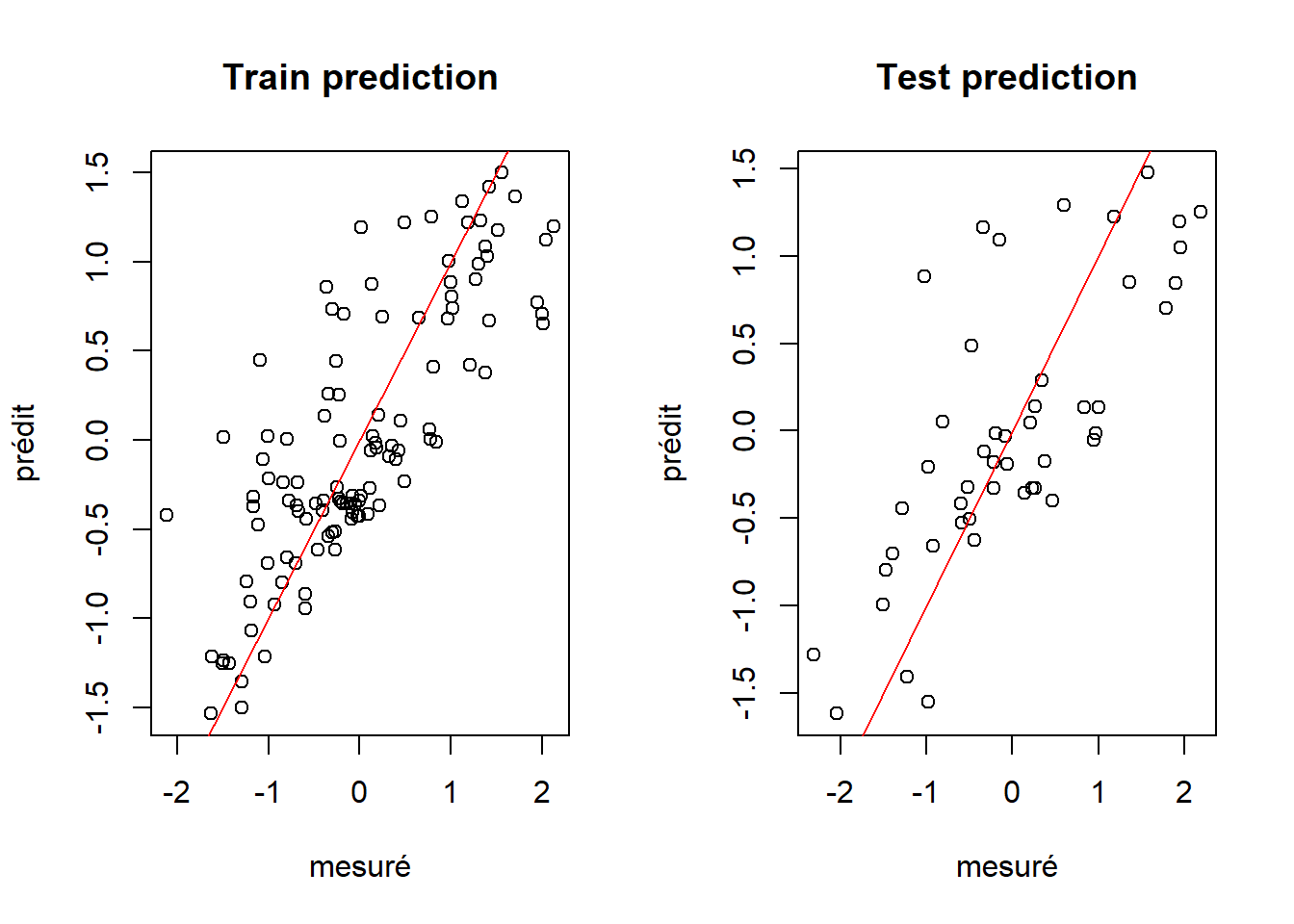
Figure 13.5: Performance du processus gaussien en entraînement et en test.
La prédiction n’est pas extraordinaire, mais gardons-la pour l’exemple (j’ai essayé avec des réseaux neuronaux sans plus de succès). La prochaine étape est de créer une gille où chaque point [longitude, latitude] servira de variable explicative pour calculer les degrés-jour.
grid <- expand.grid(lon = seq(from = -80, to = -60, by = 0.25),
lat = seq(from = 45, to = 50, by = 0.25))
grid <- grid %>%
mutate(pred_dd_mean = predict(dd_gp, newdata = ., type = "response") * sd(weather_dd$degree_days) + mean(weather_dd$degree_days),
pred_dd_sd = predict(dd_gp, newdata = ., type = "sdeviation") * sd(weather_dd$degree_days))
head(grid)## lon lat pred_dd_mean pred_dd_sd
## 1 -80.00 45 677.8054 53.88231
## 2 -79.75 45 661.8149 49.89197
## 3 -79.50 45 645.9798 46.21914
## 4 -79.25 45 630.5447 42.87580
## 5 -79.00 45 615.7486 39.86670
## 6 -78.75 45 601.8202 37.18911Utilisons les polygones de la carte du monde zoomée à l’endroit qui nous intéresse, et ajoutons-y notre prédiction superposée par les localisations des stations météo. J’ajoute des contours ainsi que des étiquettes de contours (ce qui nécessite le module metR). Les processus gaussiens permettent de juxtaposer une carte des écart-type des prédictions, donnant une appréciation de la précision du modèle (figure ??). Cette juxtaposition est effectuée avec la fonction plot_grid() le module cowplot.
##
## Attaching package: 'metR'## The following object is masked from 'package:kernlab':
##
## cross## The following object is masked from 'package:aqp':
##
## denormalize## The following object is masked from 'package:greta':
##
## f## The following object is masked from 'package:purrr':
##
## crossgg_mean <- ggplot(grid, aes(x = lon, y = lat)) +
xlim(c(-80, -60)) + ylim(c(45, 50)) + coord_equal() +
geom_tile(aes(fill = pred_dd_mean)) +
geom_contour(data = grid, mapping = aes(x = lon, y = lat, z = pred_dd_mean), binwidth = 50, colour = "black", lwd = 0.2) +
geom_label_contour(aes(z = pred_dd_mean)) +
geom_path(data = world, aes(x = long, y = lat, group = group)) +
geom_point(data = weather, mapping = aes(x = lon, y = lat), size = 0.1) +
scale_fill_gradient(low = "#8CBFE6", high = "#FF0099", na.value = "grey80")
gg_sd <- ggplot(grid, aes(x = lon, y = lat)) +
xlim(c(-80, -60)) + ylim(c(45, 50)) + coord_equal() +
geom_tile(aes(fill = pred_dd_sd)) +
geom_contour(data = grid, mapping = aes(x = lon, y = lat, z = pred_dd_sd), binwidth = 50, colour = "black", lwd = 0.2) +
geom_label_contour(aes(z = pred_dd_sd)) +
geom_path(data = world, aes(x = long, y = lat, group = group)) +
geom_point(data = weather, mapping = aes(x = lon, y = lat), size = 0.1) +
scale_fill_gradient(low = "#8CBFE6", high = "#FF0099", na.value = "grey80")
cowplot::plot_grid(gg_mean, gg_sd, labels = c("A", "B"), nrow = 2)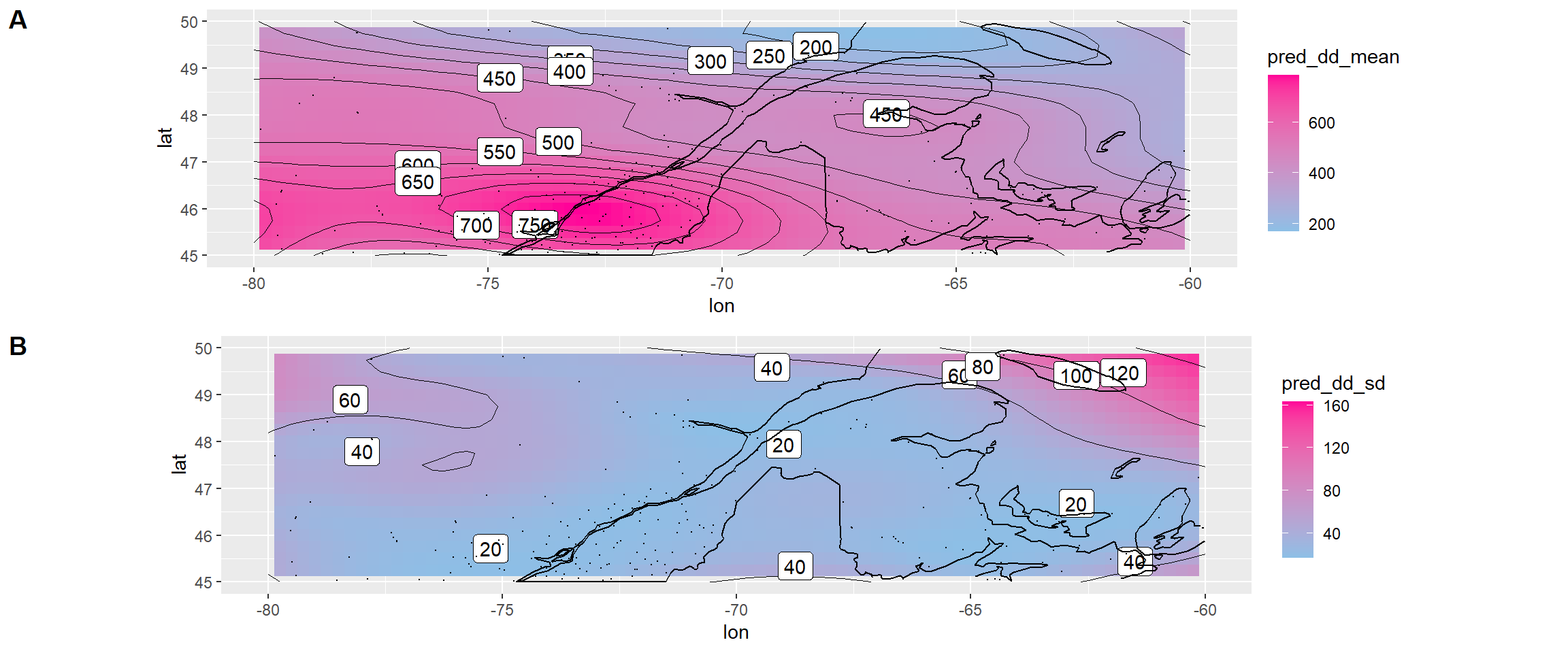
Figure 13.6: Prédiction des degrés-jour dans l’espace avec les processus gaussiens
13.7 Les objets spatialisés en R
Au chapitre 12, nous avons couvert le type d’objet ts, spécialisé pour les séries temporelles. De même, le type d’objet sf est spécialisé pour les objets georéférencés. Les formats de données spatiales conventionnellement utilisés en R depuis 2003 sont offerts par le module sp. Ce format héritait de difficultés, récemment surmontées par le module sf, plus convivial et mieux adapté au tidyverse. Bien que sp soit plus largement documenté, sf est suffisamment mature pour une utilisation professionnelle. Évidemment, un aide-mémoire a été créé (figure ??).
, créé par RStudio](images/12_sf-cheatsheet_canvas.png)
Figure 13.7: Aide-mémoire du module sf, créé par RStudio
Nous avons couvert quatre types de données spatiales. Nous allons maintenant les traiter en deux catégories:
- les données vectorielle, comprenant les points, lignes et polygones et
- les données raster, comprenant les grilles de données.
13.7.1 Données vectorielles (points, lignes et polygones)
Un cas typique consiste à importer un tableau de données localisées en un point, que l’on désire localiser en format sf avec la fonction st_as_sf(). Le tableau weather, par exemple, comporte une latitude (colonne lat) et une longitude (colonne lon), spécifiées dans l’argument coord. Puisqu’il s’agit de données canadiennes, je suppose que les coordonnées sont projetées en format NAD83, tel qu’utilisé par Statistique Canada et Ressources naturelles Canada (à défaut de trouver la bonne info en ce moment). Le code PROJ4, spécifié sous l’argument crs, décrit l’ellipsoïde utilisé pour calculer les longitudes et latitudes ainsi que, s’il y a lieu, la projection (détails plus loin dans la section 13.8).
## Linking to GEOS 3.6.1, GDAL 2.2.3, PROJ 4.9.3weather_geo <- weather %>%
st_as_sf(coords = c("lon", "lat"), crs = "+proj=longlat +datum=NAD83")
weather_geo## Simple feature collection with 260 features and 6 fields
## geometry type: POINT
## dimension: XY
## bbox: xmin: -79.85 ymin: 45.02 xmax: -60.04 ymax: 49.84
## CRS: +proj=longlat +datum=NAD83
## # A tibble: 260 x 7
## station_id station_name prov degree_days cumul_precip sdi geometry
## <dbl> <chr> <chr> <dbl> <dbl> <dbl> <POINT [°]>
## 1 10247 ILE AUX GRUES QC NA NA NA (-70.53 47.07)
## 2 10661 NORTHEAST MARGAREE (AUT) NS 372. 222. 0.904 (-60.98 46.37)
## 3 10732 NICOLET QC 823. 78.4 0.704 (-72.66 46.23)
## 4 10761 MCTAVISH QC 915. 107 0.740 (-73.58 45.5)
## 5 10762 STE-CLOTILDE QC 860. 85.2 0.820 (-73.68 45.17)
## 6 10763 ILES DE LA MADELEINE QC 326. 167. 0.853 (-61.77 47.43)
## 7 10764 TROIS-RIVIERES QC 753. 72.2 0.731 (-72.52 46.35)
## 8 10791 MATAGAMI QC 343. 72.4 0.745 (-77.79 49.76)
## 9 10792 GRAND ETANG NS 268. NA NA (-61.05 46.55)
## 10 10797 MISTOOK QC 426. NA NA (-71.72 48.6)
## # ... with 250 more rowsNotre objet sf comprend des métadonnées sur le type de géométrie (geometry type: POINT), les limites des objets (bbox: ...), le système de référence (epsg ou proj4string: ...) ainsi que le tableau descriptif. En format sf, la colonne geometry (qui elle est de type sfc) comprend dans chacune des cellules, exprimée sous forme de liste, toute l’information nécessaire à la construction de la géométrie, que ce soit un point, une ligne ou un polygone.
Pour ce qui est des polygones et des lignes, il est plus commun de les importer depuis des sources institutionnelles. On pourra télécharger des données géographiques, puis dézipper les fichier manuellement. Mais on peut aussi copier un lien, le coller dans R et dézipper automatiquement. Le block de code suivant télécharge un dossier de shapefiles décrivant les polygones des régions administratives du Québec.
download.file("ftp://ftp.mrnf.gouv.qc.ca/public/dgig/produits/bdga5m/vectoriel/region_admin_SHP.zip",
destfile="data/12_quebec/12_region_admin_SHP.zip")
unzip("data/12_quebec/12_region_admin_SHP.zip", exdir = "data/12_quebec")Pour charger dans R des shapefiles en format sf, nous utilisons la fonction st_read() pointant vers le fichier .shp.
## Reading layer `region_admin_polygone' from data source `C:\Users\serge\Documents\GitHub\ecologie-mathematique-R\data\12_quebec\region_admin_polygone.shp' using driver `ESRI Shapefile'
## Simple feature collection with 21 features and 10 fields
## geometry type: POLYGON
## dimension: XY
## bbox: xmin: -79.7625 ymin: 44.99136 xmax: -56.93495 ymax: 62.58217
## CRS: 4269## Simple feature collection with 6 features and 10 fields
## geometry type: POLYGON
## dimension: XY
## bbox: xmin: -79.7625 ymin: 48.04944 xmax: -56.93495 ymax: 62.58217
## CRS: 4269
## AREA PERIMETER REGIO_S_ REGIO_S_ID RES_NO_IND RES_DE_IND RES_CO_REG
## 1 1.240869e+02 94.6754067 2 1 50 02 0100 000 Région administrative 10
## 2 7.530857e-04 0.1519356 3 2 50 02 0100 000 Région administrative 09
## 3 4.460926e+01 55.8047474 4 3 50 02 0100 000 Région administrative 09
## 4 5.028808e-01 8.8274338 5 4 50 02 0100 000 Région administrative 09
## 5 8.779790e-02 2.0259021 6 5 50 02 0100 000 Région administrative 09
## 6 3.813094e+00 22.6943449 7 2 50 02 0100 000 Région administrative 09
## RES_NM_REG RES_CO_REF RES_CO_VER geometry
## 1 Nord-du-Québec BDGA5M V2017-06 POLYGON ((-77.80893 62.4465...
## 2 Côte-Nord BDGA5M V2017-06 POLYGON ((-66.6878 55.00005...
## 3 Côte-Nord BDGA5M V2017-06 POLYGON ((-70.02987 55.0000...
## 4 Côte-Nord BDGA5M V2017-06 POLYGON ((-66.25978 55.0000...
## 5 Côte-Nord BDGA5M V2017-06 POLYGON ((-67.2192 55.00003...
## 6 Côte-Nord BDGA5M V2017-06 POLYGON ((-63.60572 52.8760...Nous avons vu au chapitre 3 qu’il est préférable d’éviter la répétition de l’information. Dans le format tibble que nous avons utilisé pour décrire les polygones, l’information attachée à un polygone est répétée pour chaque point qui le compose: forcer une information hiérarchisée à se conformer à une structure rectangulaire multiplie la quantité d’information. Le format sf évite cette mutiplication d’information en hiérachisant les polygones dans la colonne geometry.
En guise d’exploration rapide, la fonction plot() affichera les choroplèthes.
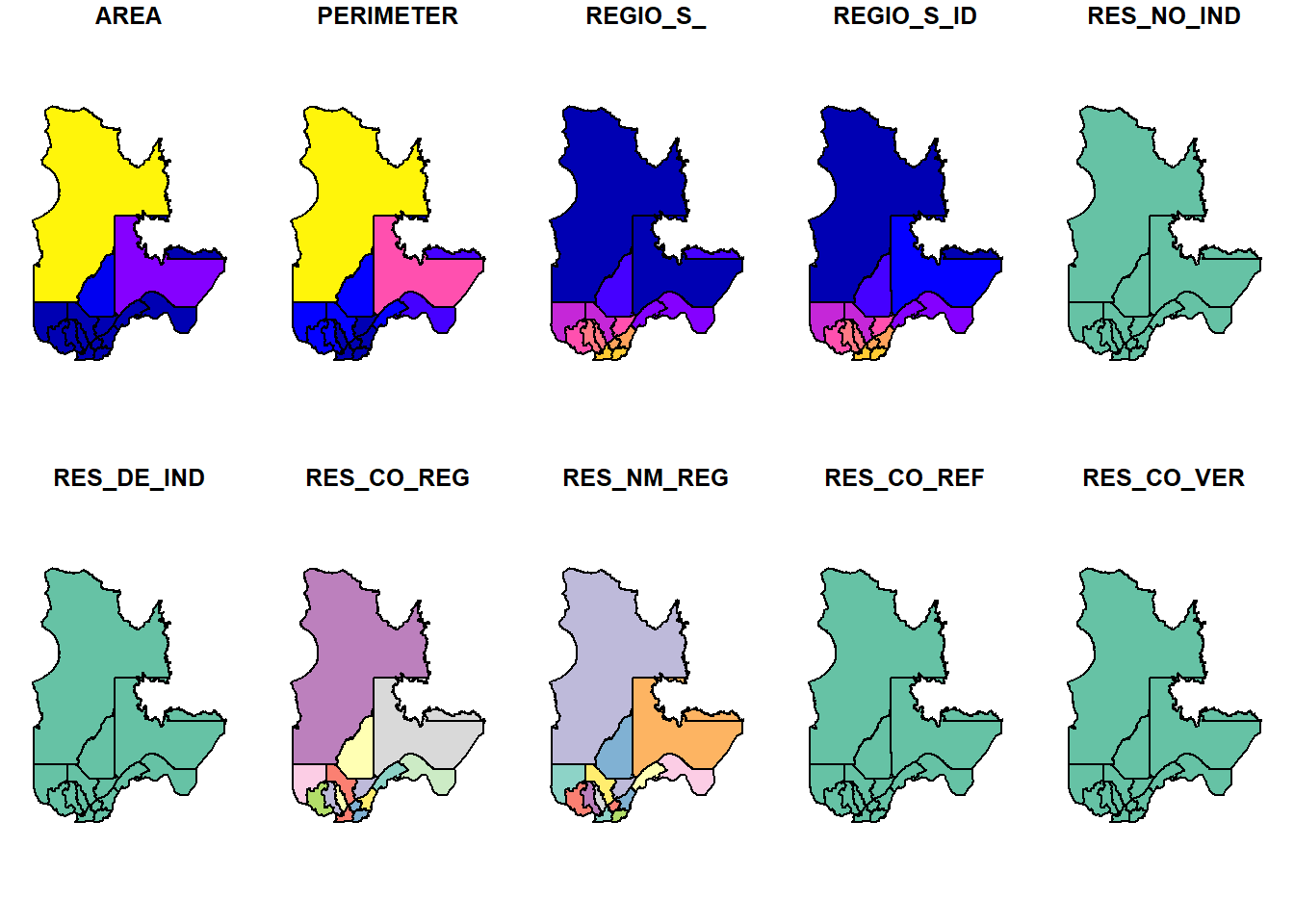
Si nous ne désirons que la géométrie,
quebec %>%
st_geometry() %>%
plot() # ou bien plot(st_geometry(quebec)), ou bien plot(quebec %>% select(geometry))
Exercice. Explorer l’objet quebec, en particulier la colonne geometry, notamment en utilisant la fonction str().
Vous pourrez soutirer les informations du système de coordonnées avec la fonction st_crs(). Il est possible de calculer des attributs des géométries à l’aide des fonctions st_area() pour les polygones, ou st_length() pour les lignes et les polygones et la fonction st_centroid() pour trouver le centroïde d’un polygone - à cette étape, il se pourrait que R vous demande d’installer le module lwgeom: suivez ses consignes!
quebec_point <- quebec %>%
mutate(st_area = st_area(quebec),
st_length = st_length(quebec)) %>%
st_centroid()## Warning in st_centroid.sf(.): st_centroid assumes attributes are constant over geometries of x## Warning in st_centroid.sfc(st_geometry(x), of_largest_polygon = of_largest_polygon):
## st_centroid does not give correct centroids for longitude/latitude data## Warning: plotting the first 9 out of 12 attributes; use max.plot = 12 to plot all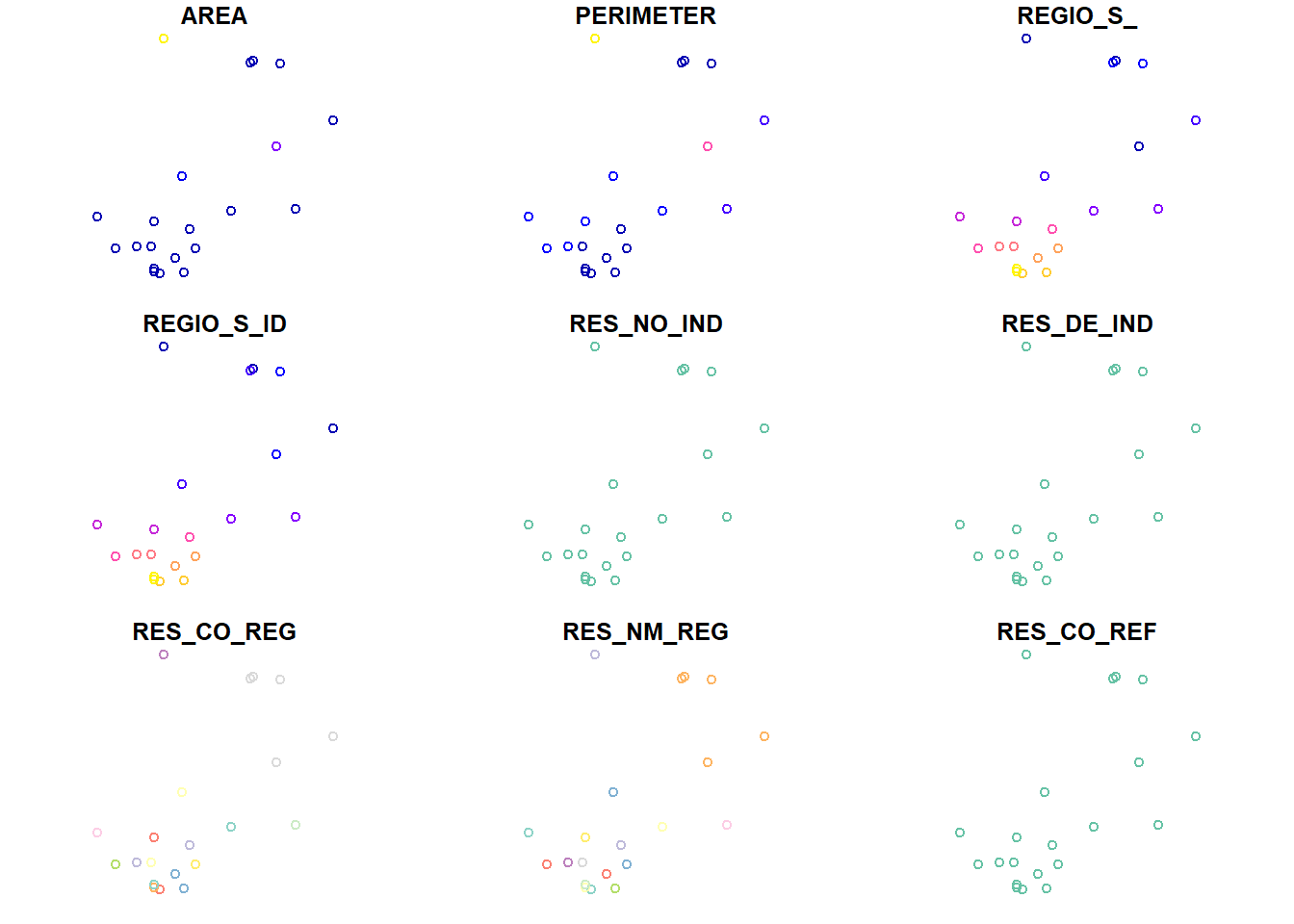
Les aires et les périmètres calculés ne correspondent pas tout à fait à ceux des variables AREA et PERIMETER, probablement calculés sur une autre base. La fonction st_centroid() crée un nouveau tableau dont la géométrie est le POINT, elle doit donc être passée après les opérations sur les polygones.
La fonction st_simplify() permet de simplifier les polygones en un nombre réduit de points, ce qui peut être utile pour accélérer les calculs. La fonction st_buffer() permet de créer un rayon d’une longueur donnée autour d’un point, procédure souvent utilisée pour visualiser un rayon d’influence. Mais pour calculer des distances, les données doivent projetées. Nous pouvons les projeter avec st_transform() avec le code EPSG désiré.
## Warning: plotting the first 10 out of 12 attributes; use max.plot = 12 to plot all
D’autres opérations sur les vecteurs sont offertes et documentées sous la fiche d’aire sf::geos_unary().
Enfin, pour exporter un tableau sf en format csv incluant la géométrie, utilisez st_write(obj = tableau,dsn = "tableau.csv", layer_options = "GEOMETRY=AS_XY"). Toutefois, si la géométrie n’est pas consituée de points, il faudra préalablement transformer les polygones en points avec st_cast().
13.7.2 Données raster
Les données rasters sont des grilles, souvent enchâssées dans des images tif géoréférencées. Ces images peuvent comprendre plusieurs variables, que l’on nomme des bandes, en référence aux bandes spectrales des images satélitaires (rouge, vert et bleu). Les données raster peuvent être importées dans votre session grâce à deux fonctions du module raster : raster() importera des données raster à une bande et brick(), des données raster à plusieurs bandes. Assurez-vous aussi que le module rgdal est bien installé.
library("raster")
library("rgdal")
canopy <- raster("data/12_nytrees/canopy.tif") # source: https://assets.datacamp.com/production/repositories/738/datasets/79cb56df0fa27272e16b366a697aba8ac1d3e923/canopy.zip
canopy## class : RasterLayer
## dimensions : 230, 253, 58190 (nrow, ncol, ncell)
## resolution : 300, 300 (x, y)
## extent : 1793685, 1869585, 2141805, 2210805 (xmin, xmax, ymin, ymax)
## crs : +proj=aea +lat_1=29.5 +lat_2=45.5 +lat_0=23 +lon_0=-96 +x_0=0 +y_0=0 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs
## source : C:/Users/serge/Documents/GitHub/ecologie-mathematique-R/data/12_nytrees/canopy.tif
## names : canopy
## values : 0, 255 (min, max)manhattan <- brick("data/12_nytrees/manhattan/manhattan.tif") # source: https://assets.datacamp.com/production/repositories/738/datasets/30830f8ba4a60aa1711f41e9a842b22cba3204f3/manhattan.zip
manhattan## class : RasterBrick
## dimensions : 773, 801, 619173, 3 (nrow, ncol, ncell, nlayers)
## resolution : 29.98979, 30.00062 (x, y)
## extent : 575667.9, 599689.7, 4503277, 4526468 (xmin, xmax, ymin, ymax)
## crs : +proj=utm +zone=18 +datum=WGS84 +units=m +no_defs +ellps=WGS84 +towgs84=0,0,0
## source : C:/Users/serge/Documents/GitHub/ecologie-mathematique-R/data/12_nytrees/manhattan/manhattan.tif
## names : manhattan.1, manhattan.2, manhattan.3
## min values : 0, 0, 0
## max values : 255, 255, 255Les informations des objets RasterLayer et RasterBrick peuvent être extraites par les fonctions extent(), ncell(), nlayers() et crs(). La fonction plot() permet d’explorer les données en créant un graphique par bande.
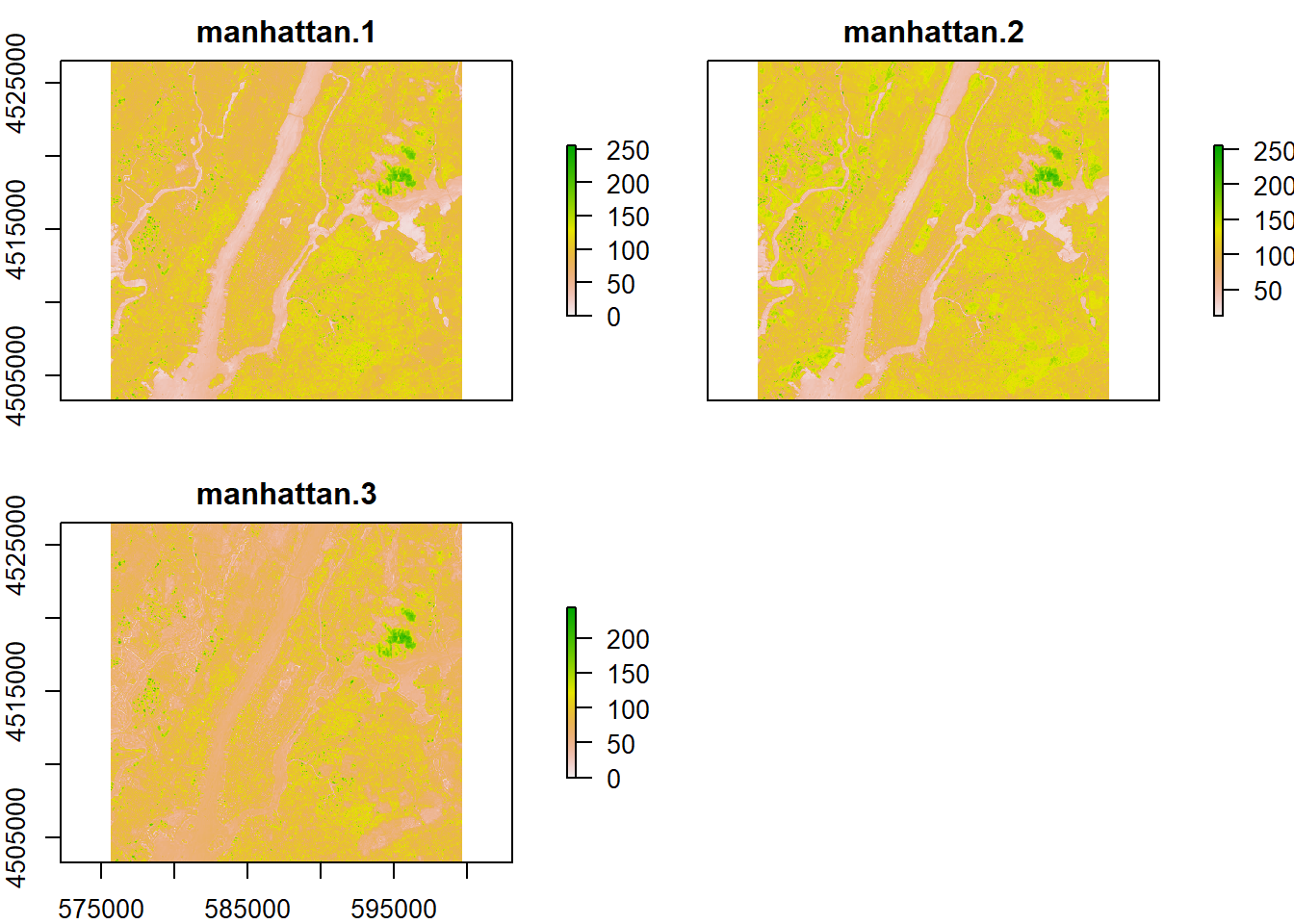
Les fichiers raster, en format qui viennent souvent en format tif, sont typiquement très volumineux. Si une plus faible résolution convient à une analyse spatiale, on pourra simplifier un raster avec la fonction raster::aggregate() (j’utilise la notation module::fonction() pour éviter la confusion avec la fonction dplyr::aggregate()). L’argument fact est le facteur de conversion et l’argument fun est la fonction d’aggrégation (typiquement mean ou median).
## class : RasterBrick
## dimensions : 39, 41, 1599, 3 (nrow, ncol, ncell, nlayers)
## resolution : 599.7958, 600.0124 (x, y)
## extent : 575667.9, 600259.5, 4503067, 4526468 (xmin, xmax, ymin, ymax)
## crs : +proj=utm +zone=18 +datum=WGS84 +units=m +no_defs +ellps=WGS84 +towgs84=0,0,0
## source : memory
## names : manhattan.1, manhattan.2, manhattan.3
## min values : 13, 30, 47
## max values : 186, 194, 185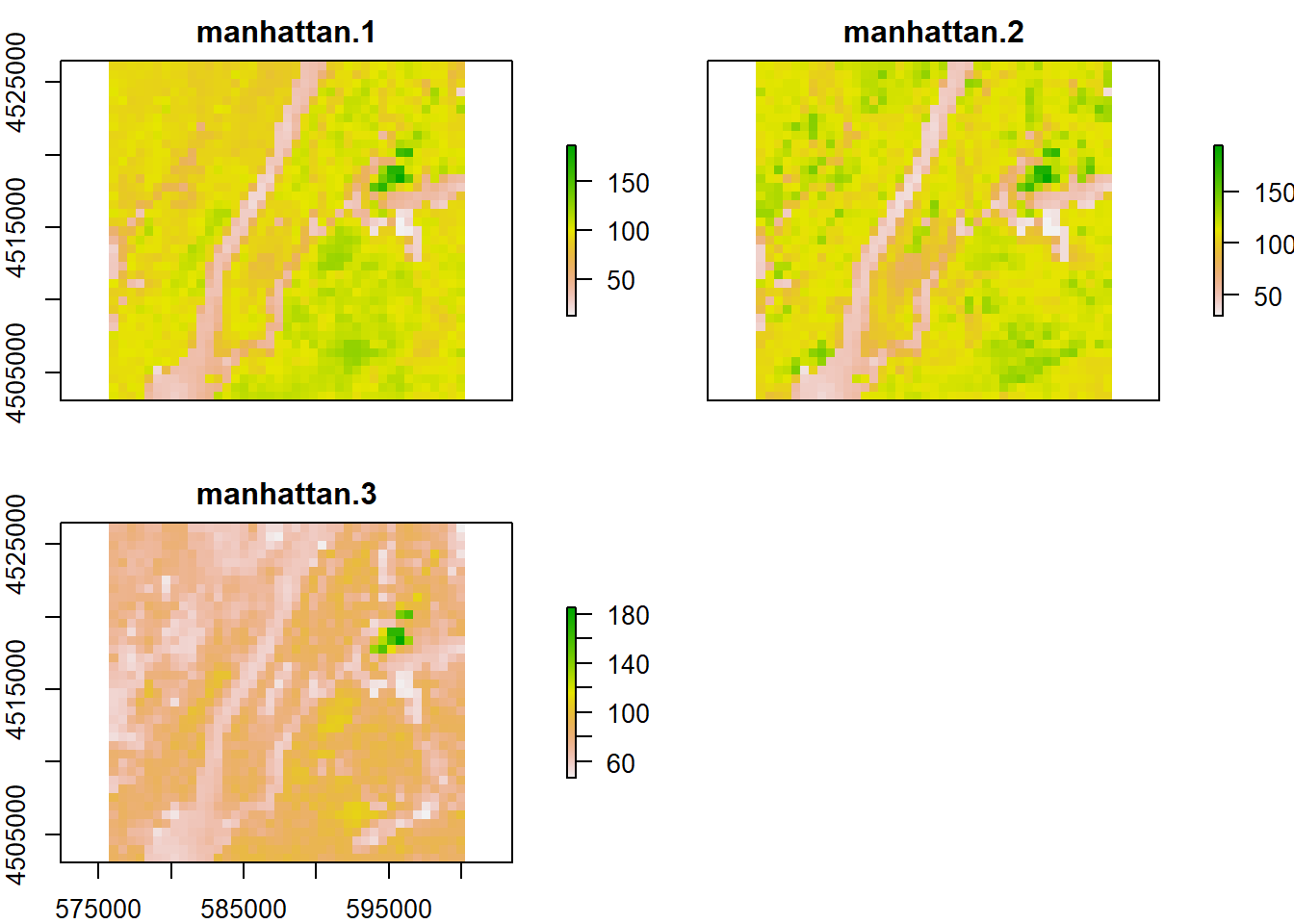
Avec un facteur de conversion de 20, nous sommes passés d’une grille de 773 \(\times\) 801 à 39 \(\times\) 41. L’exemple utilisé est volontairement exagéré pour montrer l’effet de la perte de résolution, et généralement le facteur de conversion utilisé est plus faible que 20.
La fonction reclassify() est l’équivalent de cut() pour les rasters. L’argument demandé, en plus de l’objet raster, est une matrice de classification à trois colonnes. Les deux premières colonnes spécifient la plage de valeur à classifier et la troisième colonne spécifie la valeur de remplacement (qui peut être NA). La classification s’applique à toutes les couches s’il s’agit d’un RasterBrick.
manhattan_rcl <- reclassify(manhattan_lowres,
rcl = matrix(c(0, 50, 1,
50, 100, 2,
100, 1000, NA),
ncol = 3, byrow = TRUE))
plot(manhattan_rcl)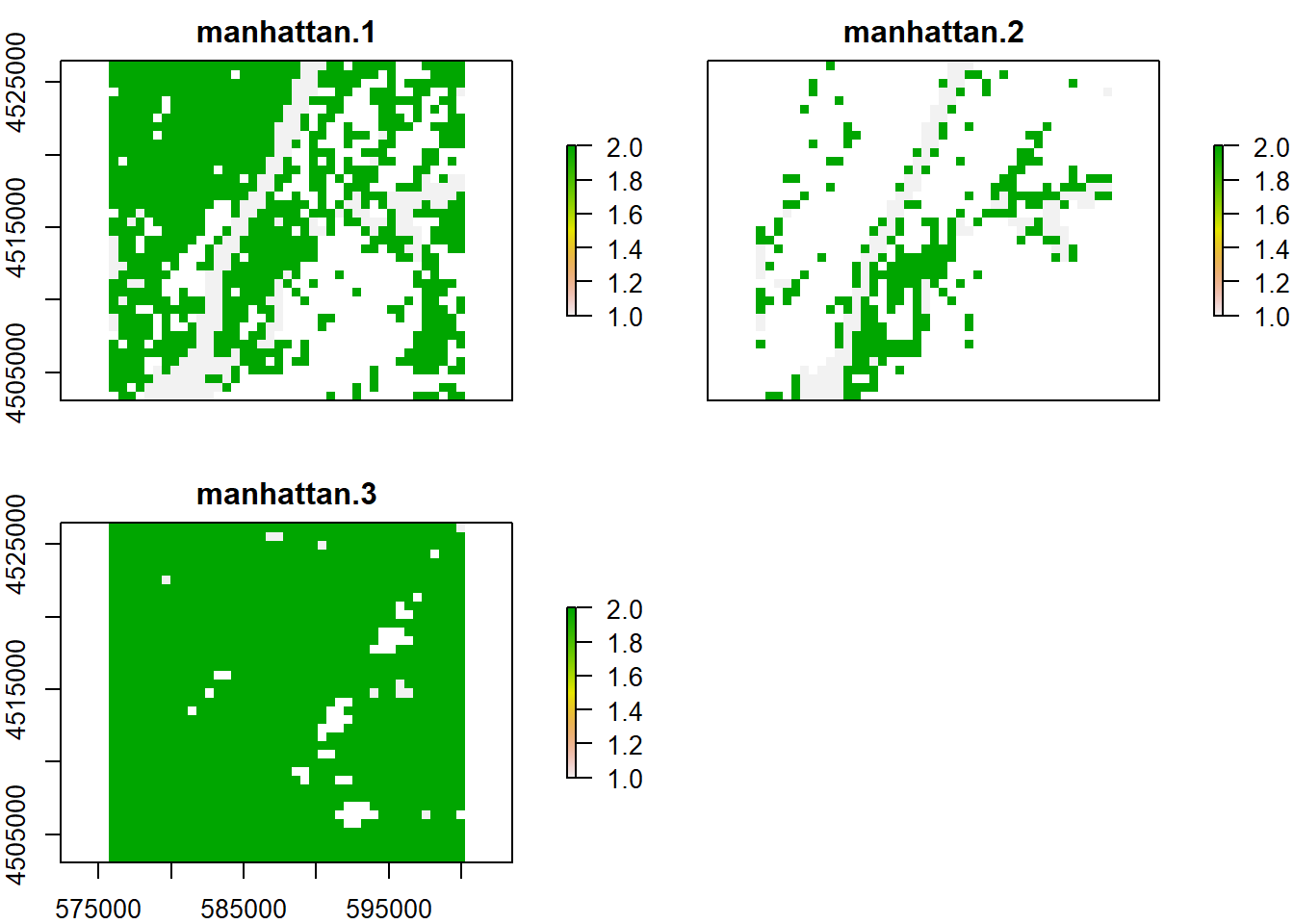
13.8 Les systèmes de coordonnées
Les longitudes et latitudes sont des angles sur un ellipsoïde de révolution. Différentes institutions utilisent différentes formes d’ellipsoïde portant leur nom particulier: NAD83, WGS84, ETRS89, etc. Les projections servent à aplanir des coordonnées géodésiques obtenues selon un ellipsoïde donné en vue de créer des représentations 2D, comme la projection Mercator universelle ou de nombreuses autres. Le système de coordonnées peut être projeté ou non.
- Système de coordonnées non-projetées: caractérisé par des angles de longitude et de latitudes sur un système géodésique 3D représenté par un ellipsoïde de révolution.
- Système de coordonnées projetées: caractérisé par des distances X et Y sur une système géodésique représenté en 2D.
Lorsque vous utilisez des shapefiles, les informations du système de coordonnées seront incluses dans le fichier ayant une extension prj. Examinons le système de coordonnées du tableau quebec avec la fonction st_crs().
## Coordinate Reference System:
## User input: 4269
## wkt:
## GEOGCS["GCS_North_American_1983",
## DATUM["North_American_Datum_1983",
## SPHEROID["GRS_1980",6378137.0,298.257222101]],
## PRIMEM["Greenwich",0.0],
## UNIT["Degree",0.0174532925199433],
## AUTHORITY["EPSG","4269"]]D’emblée, la mention +proj=longlat retrouvée dans proj4string (une représentation de PROJ4) indique que le système n’est pas projeté, et que le système géodésique est le GRS80, pratiquement identique au WGS84. Le code EPSG contient la même information que le proj4string, traduite de manière succincte par un code à 4 chiffres. Dans certains cas, les informations du système de coordonnées ne sont pas disponibles: il vous faudra creuser si elles sont essentielles à vos travaux. Pour assigner un système de coordonnées, vous pourrez soit assigner l’EPSG par st_crs(objet_sg) <- 4269 ou objet_sg <- objet_sg %>% st_set_crs(), ou bien le PROJ4 par st_crs(objet_sg) <- "+proj=longlat +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +no_defs". La procédure est la même pour les rasters, mais avec la fonction crs() au lieu de st_crs().
Pour passer d’un système de coordonnées à un autre, utilisez st_transform() pour les vecteurs et projectRasters() pour les rasters. Pour les rasters, si vos données sont catégorielles, et non pas numérique, utilisez method = "ngb" plutôt que la valeur par défaut, method = "bilinear", conçue pour les variables numériques.
13.9 Manipuler des tableaux sf
Vous avez peut-être remarqué que j’ai précédemment effectué une opération mutate() en mode pipeline (%>%) sur un tableau sf. Eh oui, les sf sont compatibles avec le mode tidyverse. Vous pourrez filtrer avec filter(), sélectionner avec select() et manipuler des colonnes avec mutate(). Reprenons les données des espèces en danger, mais cette fois-ci nous allons travailler avec des données spatialisées avec sf. D’abord, allons chercher une carte du monde: le format geojson peut être importé de la même manière que des shape files. Puisqu’un geojson consigne l’information géographique en un seul fichier (les shapefiles en contiennent plusieurs), on peut l’importer directement d’Internet.
## Reading layer `countries.geo' from data source `https://raw.githubusercontent.com/johan/world.geo.json/master/countries.geo.json' using driver `GeoJSON'
## Simple feature collection with 180 features and 2 fields
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: -180 ymin: -85.60904 xmax: 180 ymax: 83.64513
## CRS: 4326## Simple feature collection with 180 features and 2 fields
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: -180 ymin: -85.60904 xmax: 180 ymax: 83.64513
## CRS: 4326
## First 10 features:
## id name geometry
## 1 AFG Afghanistan MULTIPOLYGON (((61.21082 35...
## 2 AGO Angola MULTIPOLYGON (((16.32653 -5...
## 3 ALB Albania MULTIPOLYGON (((20.59025 41...
## 4 ARE United Arab Emirates MULTIPOLYGON (((51.57952 24...
## 5 ARG Argentina MULTIPOLYGON (((-65.5 -55.2...
## 6 ARM Armenia MULTIPOLYGON (((43.58275 41...
## 7 ATA Antarctica MULTIPOLYGON (((-59.57209 -...
## 8 ATF French Southern and Antarctic Lands MULTIPOLYGON (((68.935 -48....
## 9 AUS Australia MULTIPOLYGON (((145.398 -40...
## 10 AUT Austria MULTIPOLYGON (((16.97967 48...Des multipolygones sont formés lorsque plusieurs polygones forment une seule entité, par exemple un pays constitué de plusieurs îles. Nous allons effectué la jointure entre le tableau world_gj et les données de l’IUCN. De même que précédemment, les noms des pays doivent correspondre exactement.
iucn_oecd <- iucn_oecd %>%
replace(.=="USA", "United States of America") %>%
replace(.=="UK", "United Kingdom") %>%
dplyr::rename("name" = "region")Pour cette jointure, je désire ne conserver que les données géographiques des pays de l’OCDE. Je peux effectuer une jointure à gauche sur le tableau iucn_oecd ou une joiture à droite sur le tableau world_gj.
Contrairement aux tableaux tibble, le format sf conserve la géométrie.
## Simple feature collection with 36 features and 2 fields (with 1 geometry empty)
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: -180 ymin: -55.61183 xmax: 180 ymax: 83.23324
## CRS: 4326
## First 10 features:
## name n_threatened_species geometry
## 1 Mexico 151 MULTIPOLYGON (((-97.14001 2...
## 2 Brazil 110 MULTIPOLYGON (((-57.62513 -...
## 3 Australia 109 MULTIPOLYGON (((145.398 -40...
## 4 United States of America 78 MULTIPOLYGON (((-155.5421 1...
## 5 Canada 52 MULTIPOLYGON (((-63.6645 46...
## 6 Colombia 42 MULTIPOLYGON (((-75.37322 -...
## 7 Russia 40 MULTIPOLYGON (((143.648 50....
## 8 Chile 36 MULTIPOLYGON (((-68.63401 -...
## 9 Slovenia 34 MULTIPOLYGON (((13.80648 46...
## 10 Switzerland 34 MULTIPOLYGON (((9.594226 47...Pour une raison ou une autre, si vous désirez retirer la géométrie,
## Selecting by n_threatened_species## name n_threatened_species
## 1 Mexico 151
## 2 Brazil 110
## 3 Australia 109
## 4 United States of America 78On pourra explorer notre tableau avec la fonction plot().
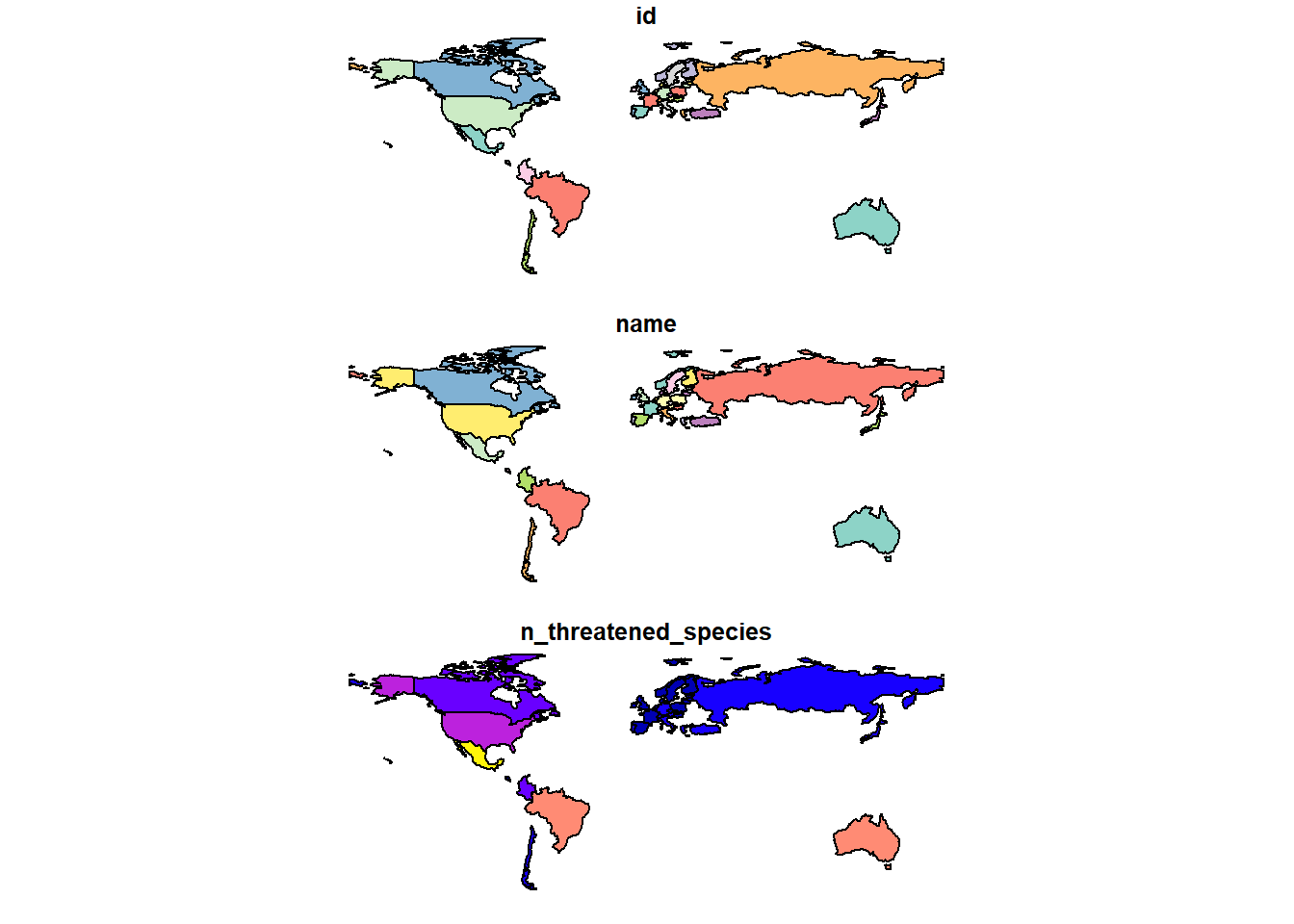
Tout comme on effectue des jointures entre des tableaux, on peut effectuerd es jointures spatiales sur des sf. On pourra trouver des intersections entre polygones, effectuer des unions, des différences, etc. Par exemple, en modélisation, il est commun d’extrapoler des résultats sur une grille. Ici, nous créons une grille couvrant tout le québec (figure ??).
- Nous créons une grille constituée des centroïdes,
%>%# (par défaut, il s’agit d’une grille de polygones rectangulaires) - nous transformons le résultat en format
sf(au lieu desfc),%>% - nous effectuons une jointure sous forme d’intersection et
%>% - nous retirons les occurences hors de la jointure.
quebec_grid <- quebec %>%
st_make_grid(n = 80, what = "centers") %>%
st_sf() %>% # transformer en objet sf
st_join(quebec, join = st_intersects) %>%
drop_na()## although coordinates are longitude/latitude, st_intersects assumes that they are planar
## although coordinates are longitude/latitude, st_intersects assumes that they are planar
## although coordinates are longitude/latitude, st_intersects assumes that they are planar
## although coordinates are longitude/latitude, st_intersects assumes that they are planarpar(mfrow = c(1, 2))
plot(quebec_grid %>% st_geometry(), pch = 16, cex = 0.2, main = "Grille Québec")
plot(quebec_grid %>% filter(RES_NM_REG == "Montérégie") %>% st_geometry(), main = "Grille Montérégie")
Pour soutirer la grille en vue de modéliser,
## # A tibble: 3,636 x 2
## lon lat
## <dbl> <dbl>
## 1 -74.2 45.1
## 2 -73.9 45.1
## 3 -73.6 45.1
## 4 -73.3 45.1
## 5 -73.1 45.1
## 6 -72.8 45.1
## 7 -72.5 45.1
## 8 -72.2 45.1
## 9 -71.9 45.1
## 10 -71.6 45.1
## # ... with 3,626 more rows13.10 Manipuler des objets raster
Comme les objets vectoriels, les objets raster peuvent subir différents types d’opérations. Nous en couvrirons trois.
- Masque (
mask()): l’intersection entre un polygone et un raster. - Découper (
crop()): découpe rectangulaire selon les limites de l’objet. - Extraction (
extract()): extrait, et accessoirement effectue un sommaire, des rasters dans un polygone donné
Créons d’abord un polygone ayant le même système de coordonnées que le raster canopy.
poly <- st_sfc(st_polygon(list(cbind(c(1800000, 1830000, 1820000, 1800000),
c(2160000, 2200000, 2150000, 2160000))))) %>%
st_set_crs(as.character(crs(canopy))) %>%
st_cast("POLYGON")En ce moment, le module raster n’est pas adapté au format sf, qu’il faudrait préalablement convertir vers l’ancien format sp.
Appliquons un masque, puis un crop, puis les deux.
canopy_mask <- mask(canopy, mask = poly_sp)
canopy_crop <- crop(canopy, y = poly_sp)
canopy_mc <- crop(canopy_mask, y = poly_sp)
par(mfrow = c(1, 4))
plot(canopy, main = "Original")
plot(poly_sp, add = TRUE)
plot(canopy_mask, main = "mask()")
plot(poly_sp, add = TRUE)
plot(canopy_crop, main = "crop()")
plot(poly_sp, add = TRUE)
plot(canopy_mc, main = "mask() & crop()")
plot(poly_sp, add = TRUE)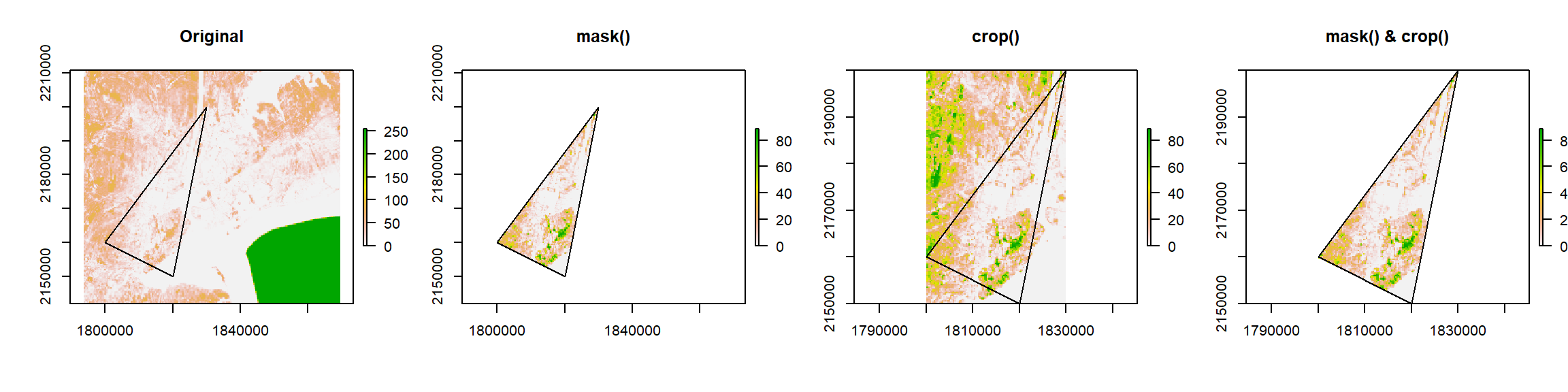
Pour effectuer un calcul sur l’intérieur du polygone avec extract()… on spécifie le raster, le polygone et la fonction!
## [,1]
## [1,] 10.5140513.11 Graphiques d’objets spatialisés
Pour afficher les objets sf et raster, nous avons utilisé les fonctions de base à titre exploratoire. Mais lorsque vient le temps de publier une carte, la trousse de ggplot2 est toute indiquée, en y ajoutant l’outil geom_sf().
Les coordonnées peuvent être manipulées avec coord_sf().
world_gj_iucn <- world_gj %>%
full_join(iucn_oecd, by = "name")
ggplot(world_gj_iucn) +
geom_sf(aes(fill = n_threatened_species), colour = "gray50") +
coord_sf(xlim = c(-170, -40), ylim = c(10, 80)) +
scale_fill_gradient(low = "#8CBFE6", high = "#FF0099", na.value = "grey80") +
labs(title = "Number of threatened species in OECD countries",
subtitle = "Source: OCDE, 2019") +
guides(fill = guide_legend(title = "Number of\nthreatened\nspecies"))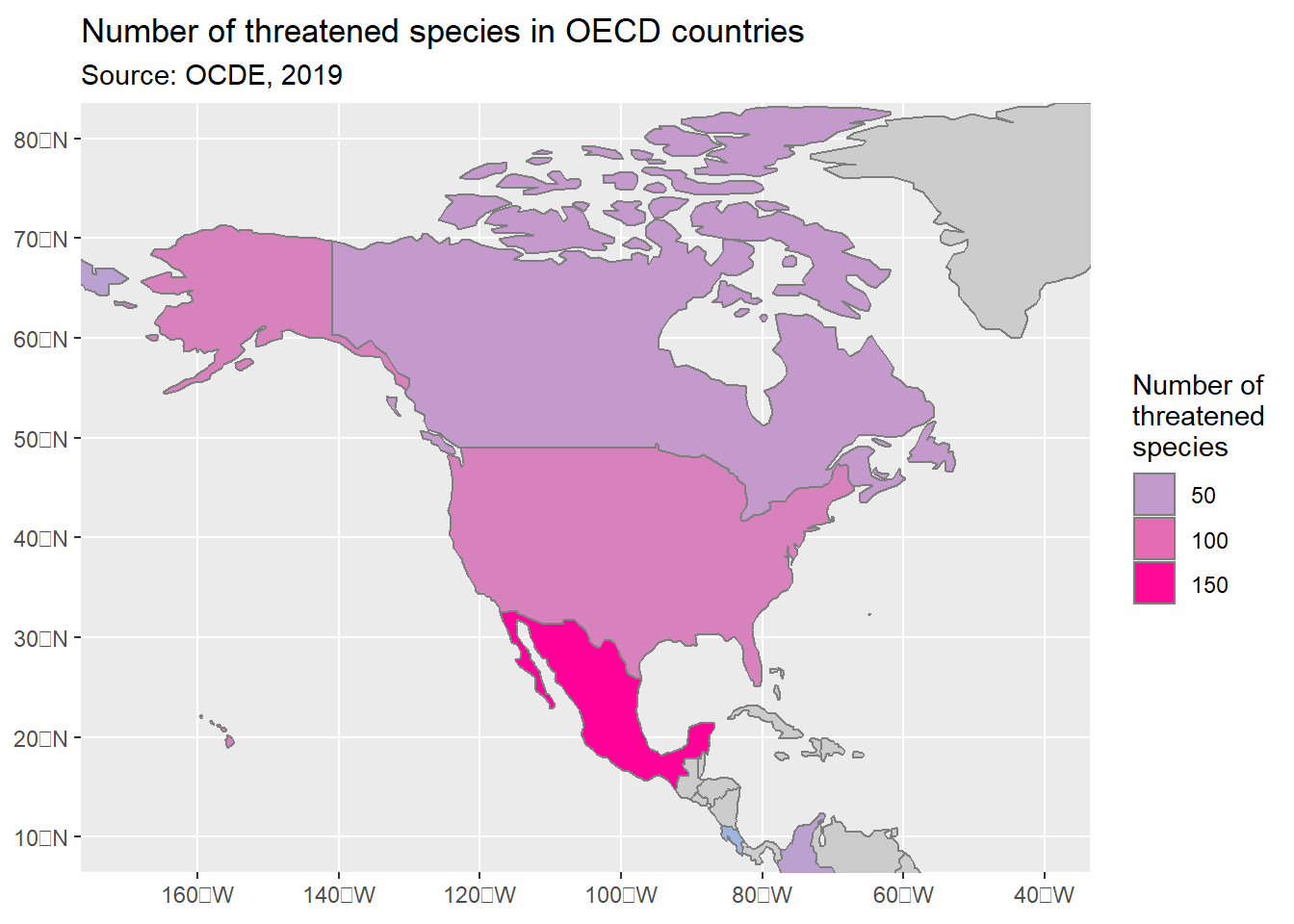
Les cartes thématiques de tmap (thematic maps) sont construites sensiblement de la même manière que ggplot2. Différents types de projections sont disponibles avec différentes palettes de couleurs (palette_explorer()).
library("tmap")
library("tmaptools")
tm_shape(set_projection(world_gj_iucn, 4326)) +
tm_polygons("n_threatened_species", palette = "viridis")## Warning: The shape set_projection(world_gj_iucn, 4326) is invalid. See sf::st_is_valid## Warning: The shape set_projection(world_gj_iucn, 4326) contains empty units.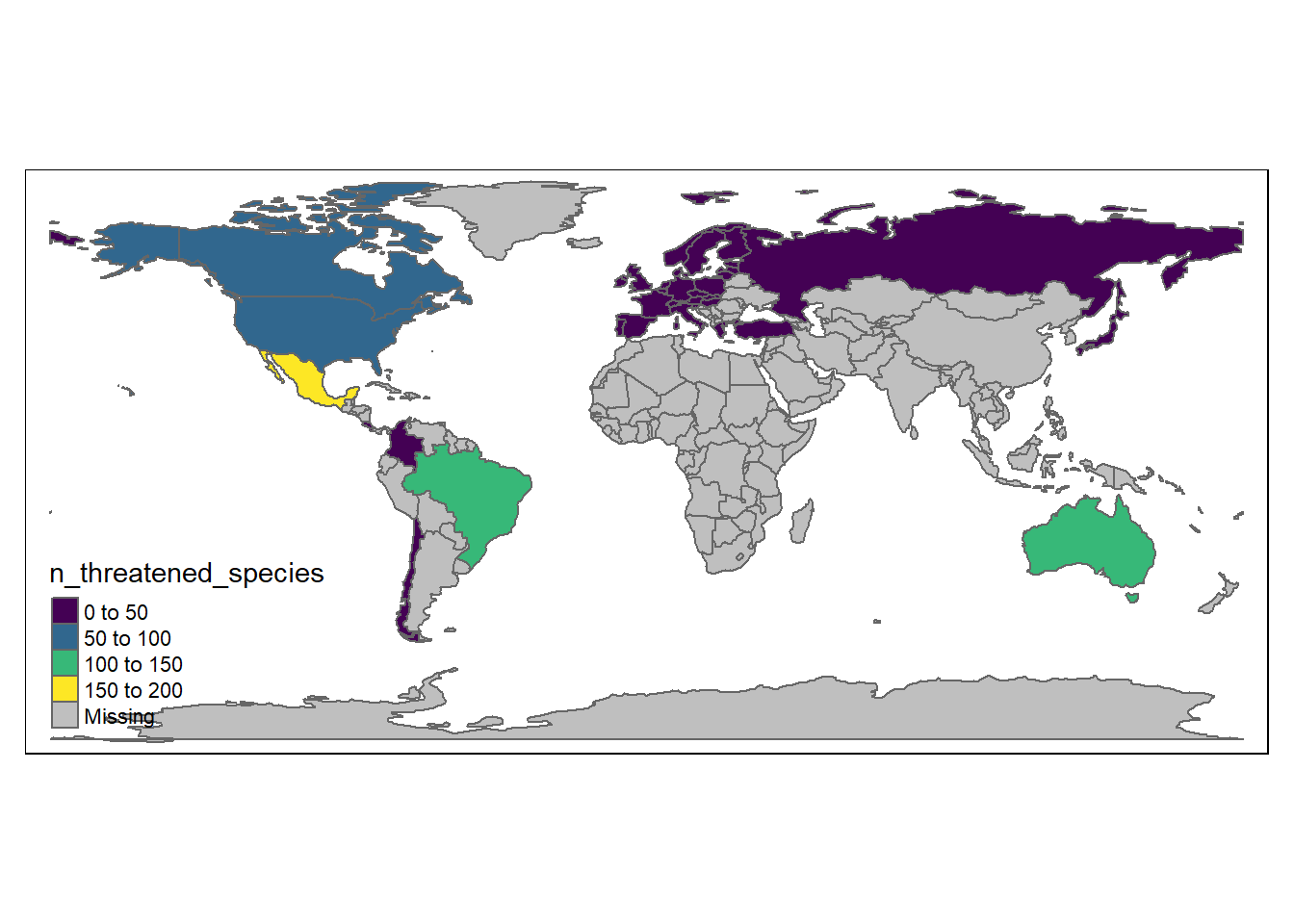
Si vous désirez créer des cartes intéractives, passez en mode leaflet en spécifiant tmap_mode("view") (pour revenir en mode statique, tmap_mode("plot"))
## tmap mode set to interactive viewing## Warning: The shape world_gj_iucn is invalid. See sf::st_is_valid## Warning: The shape world_gj_iucn contains empty units.<div id="htmlwi70a6e" style="width:100%;height:480px;" class="leaflet html-widget">
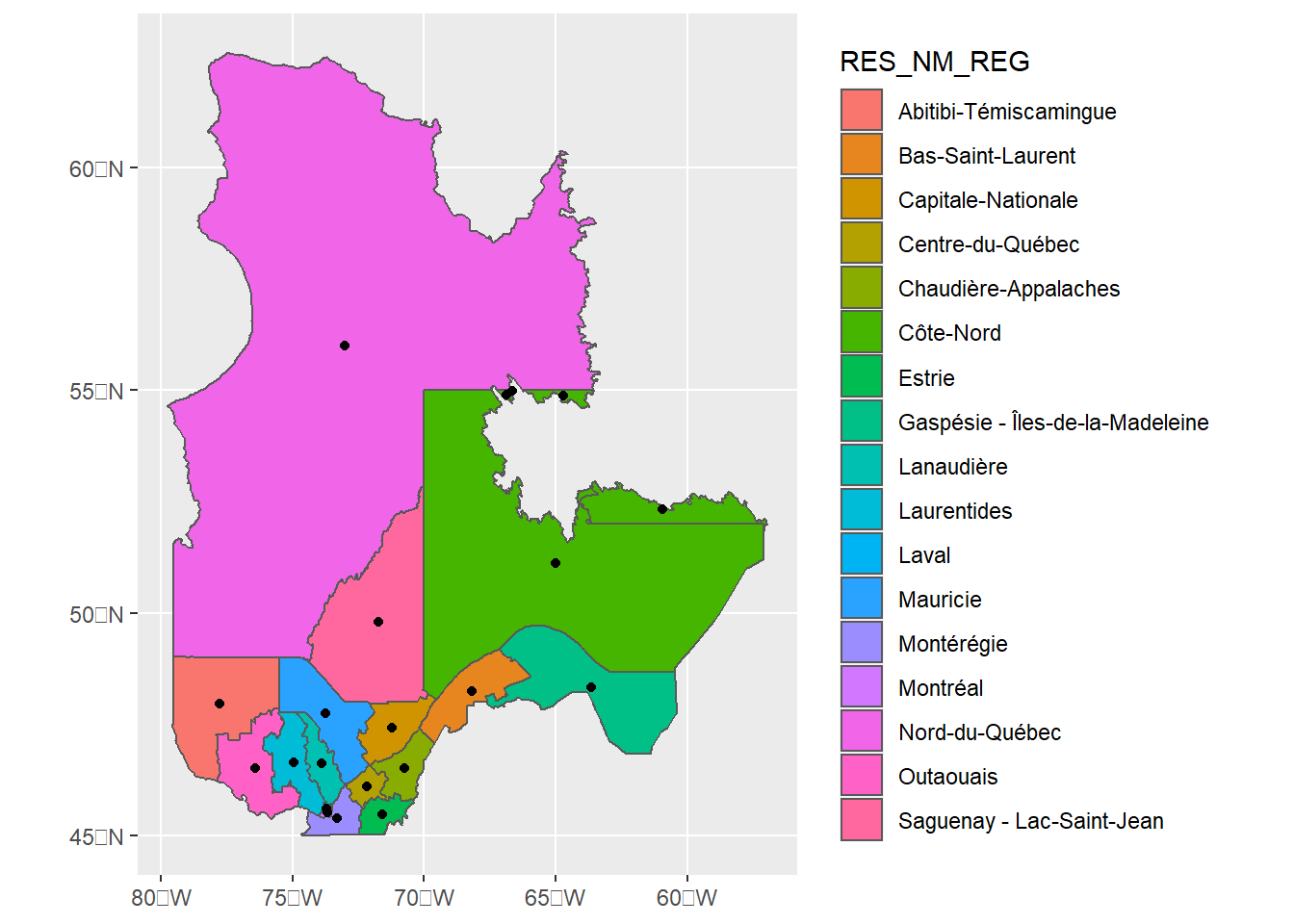
quebec_tmap <- tm_shape(quebec) +
tm_polygons(c("AREA", "PERIMETER")) +
tm_facets(sync = TRUE, ncol = 2)
quebec_tmap<div style="dis%;float:left;border-style:solid;border-color:#BEBEBE;border-width:1px 1px 1px 1px;">
## Warning in png(tmp, width = width, height = height, res = res): 'width=7, height=7' ne sont
## probablement pas des valeurs en pixels## Map saved to C:\Users\serge\Documents\GitHub\ecologie-mathematique-R\images\12_quebec_tmap.png## Resolution: 3220.011 by 2100 pixels## Size: 10.73337 by 7 inches (300 dpi)Toutefois, au moment d’écrire ces lignes, l’exportation en format dynamique ne fonctionne pas pour les facettes. De plus, il semble y avoir un bogue avec les chemins relatifs. Il faudra donc coller (paste0) le répertoire de travail (getwd()) au chemin relatif ("/images/12_quebec_tmap_widget/12_quebec_tmap.html"). Enfin, les fichiers html font souvent référence à des fichiers externes: mieux vaut les enregistrer dans des dossiers indépendants (dans ce cas dans "12_quebec_tmap_widget", que vous pourrez zipper avant de partager, ou placer sur un site web) plutôt que dans un dossier comprenant plusieurs images. Pas si compliqué… quand on le sait.
quebec_tmap_area <- tm_shape(quebec) +
tm_polygons("AREA")
tmap_save(tm = quebec_tmap_area, filename = paste0(getwd(),"/images/12_quebec_tmap_widget/12_quebec_tmap.html"))## Interactive map saved to C:\Users\serge\Documents\GitHub\ecologie-mathematique-R\images\12_quebec_tmap_widget\12_quebec_tmap.html13.12 Ressources complémentaires
- Geocomputation with R, de Robin Lovelace, Jakub Nowosad et Jannes Muenchow (2019).
- Spatial Data Science, de Robert J. Hijmans, du Geospatial and Farming Systems Research Consortium (GFC), University of California (2019)
- Simple Features for R, de Edzer Pebesma (2019)