2 L’analyse de données compositionnelles
Nous avons vu au chapitre 1 que les données compositionnelles doivent subir une transformation préalable en vue d’être analysées et modélisées. S’il faut être prudent sur l’interprétation des variables transformées, il faut aussi l’être sur les statistiques qui leur sont associées. En effet, les variables ayant subit une transformation compositionnelle peuvent être intégrés dans des flux de calculs en biostatistiques (tests d’hypothèses, modèles linéaires ou non linéaires, etc.) ou en bioheuristique (partitionnement, ordination, etc.), en passant par la détection de valeurs aberrantes et l’imputation de données manquantes.
2.1 Imputation de données manquantes
Pour toutes sortes de raison, il arrive parfois que des données soient manquantes. Les données manquantes se répartissent selon différents cas de figures (Graham, 2012; Little et Rubin, 2002) dont trois principaux:
- les valeurs manquantes univariées: pour une variable donnée, si une observation est absente, alors toutes les observations suivantes pour cette variable sont absentes (figure 2.1a).
- les valeurs manquantes monotones: la valeur d’une variable \(Y_j\) manquante pour un individu \(i\) implique que toutes les variables suivantes \(Y_k\) (\(k > j\)) sont manquantes pour cet individu (figure 2.1b).
- les valeurs manquantes arbitraires: la matrice ne dessine spécifiquement aucune des formes précédentes (figure 2.1c).
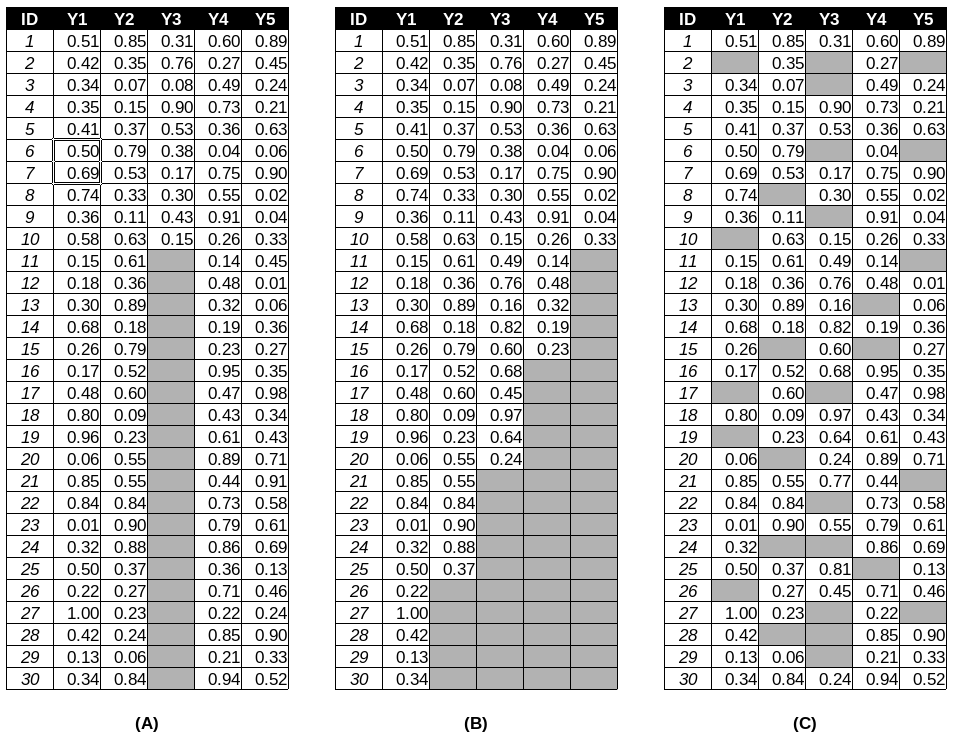
Figure 2.1: Exemple de profils de données manquantes
Le module VIM permet de visualiser la structure des données manquantes.
Pour l’exemple, prenons le tableau coffee, qui comprend la composition chimique de plusieurs échantillons associés à un cultivar, puis remplaçons au hasard des données par des valeurs manquantes (NA), puis vérifions les proportions de données manquantes et les proportions de combinaisons de données manquantes.
set.seed(867209)
data("coffee", package = "robCompositions")
coffee_NA <- coffee
n_NA <- 15
row_NA <- sample(1:nrow(coffee), n_NA, replace = TRUE)
col_NA <- sample(2:ncol(coffee), n_NA, replace = TRUE)
for (i in 1:n_NA) coffee_NA[row_NA[i], col_NA[i]] <- NA
summary(aggr(coffee_NA, sortVar = TRUE))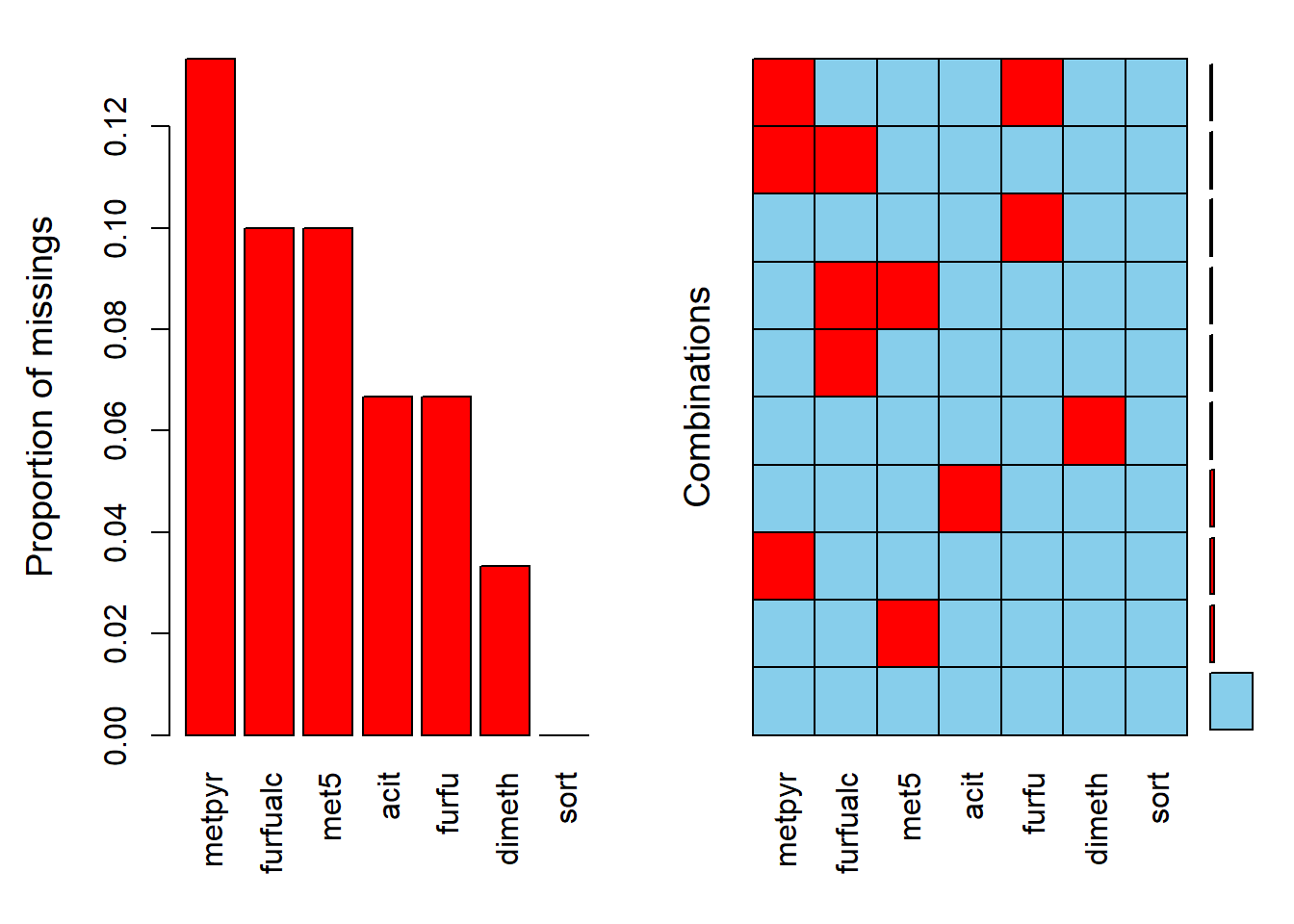
Figure 2.2: Portrait des valeurs manquantes avec VIM.
##
## Variables sorted by number of missings:
## Variable Count
## metpyr 0.13333333
## furfualc 0.10000000
## met5 0.10000000
## acit 0.06666667
## furfu 0.06666667
## dimeth 0.03333333
## sort 0.00000000##
## Missings per variable:
## Variable Count
## sort 0
## acit 2
## metpyr 4
## furfu 2
## furfualc 3
## dimeth 1
## met5 3
##
## Missings in combinations of variables:
## Combinations Count Percent
## 0:0:0:0:0:0:0 18 60.000000
## 0:0:0:0:0:0:1 2 6.666667
## 0:0:0:0:0:1:0 1 3.333333
## 0:0:0:0:1:0:0 1 3.333333
## 0:0:0:0:1:0:1 1 3.333333
## 0:0:0:1:0:0:0 1 3.333333
## 0:0:1:0:0:0:0 2 6.666667
## 0:0:1:0:1:0:0 1 3.333333
## 0:0:1:1:0:0:0 1 3.333333
## 0:1:0:0:0:0:0 2 6.666667Pour imputer les valeurs manquantes, une méthode commune est d’inspecter les valeurs des vecteurs les plus proches ne manquant pas la donnée en question et d’imputer la moyenne ou la médiane de ces valeurs (algoritmhe des KNN, que nous verrons toute à l’heure). La notion de “plus proche” imlique le calcul d’une distance. Or les distances entre compositions sont peu fiables. On pourrait imputer des ilr, mais le changement d’un ilr entraînera une perturbation d’au moins une autre concentration. La fonction robCompositions::impCoda() utilise des méthodes robustes pour imputer directement les compositions.
library("robCompositions")
coffee_imp <- impCoda(coffee_NA[, -1])$xImp
coffee_imp2.2 Détection de valeurs aberrantes
Les valeurs aberrantes peuvent avoir un effet important sur les stats. Elles sont aussi parfois une occasion d’inspecter les données et de détecter des mécanismes jusqu’alors insoupsonnés. Les données aberrantes peuvent avantageusement être détectées sur des données transformées. Encore faut-il utiliser des statistiques robustes.
library("mvoutlier")
library("ellipse")
library("ggtern")
data("coffee")
sbp <- matrix(c(1, 1,-1,
1,-1, 0),
ncol = 3,
byrow = TRUE)
coffee_comp <- coffee %>%
dplyr::select(acit, metpyr, furfu) %>%
acomp() %>%
as_tibble()
coffee_ilr <- coffee_comp %>%
ilr(., V = gsi.buildilrBase(t(sbp))) %>%
as_tibble(.) %>%
dplyr::rename(furfu_metpyr.acit = V1,
metpyr_acit = V2)
elldev_ilr <- ellipse(x = cov(coffee_ilr),
centre = apply(coffee_ilr, 2, mean),
level = 0.975) %>%
as_tibble()
mcd <- covMcd(coffee_ilr)
elldev_ilr_rob <- ellipse(x = mcd$cov,
centre = mcd$center,
level = 0.975) %>%
as_tibble()
coffee_ilr %>%
ggplot(mapping = aes(x = furfu_metpyr.acit, y = metpyr_acit)) +
geom_point() +
geom_path(data = elldev_ilr, aes(x = furfu_metpyr.acit, y = metpyr_acit), colour = "red") +
geom_path(data = elldev_ilr_rob, aes(x = furfu_metpyr.acit, y = metpyr_acit), colour = "green")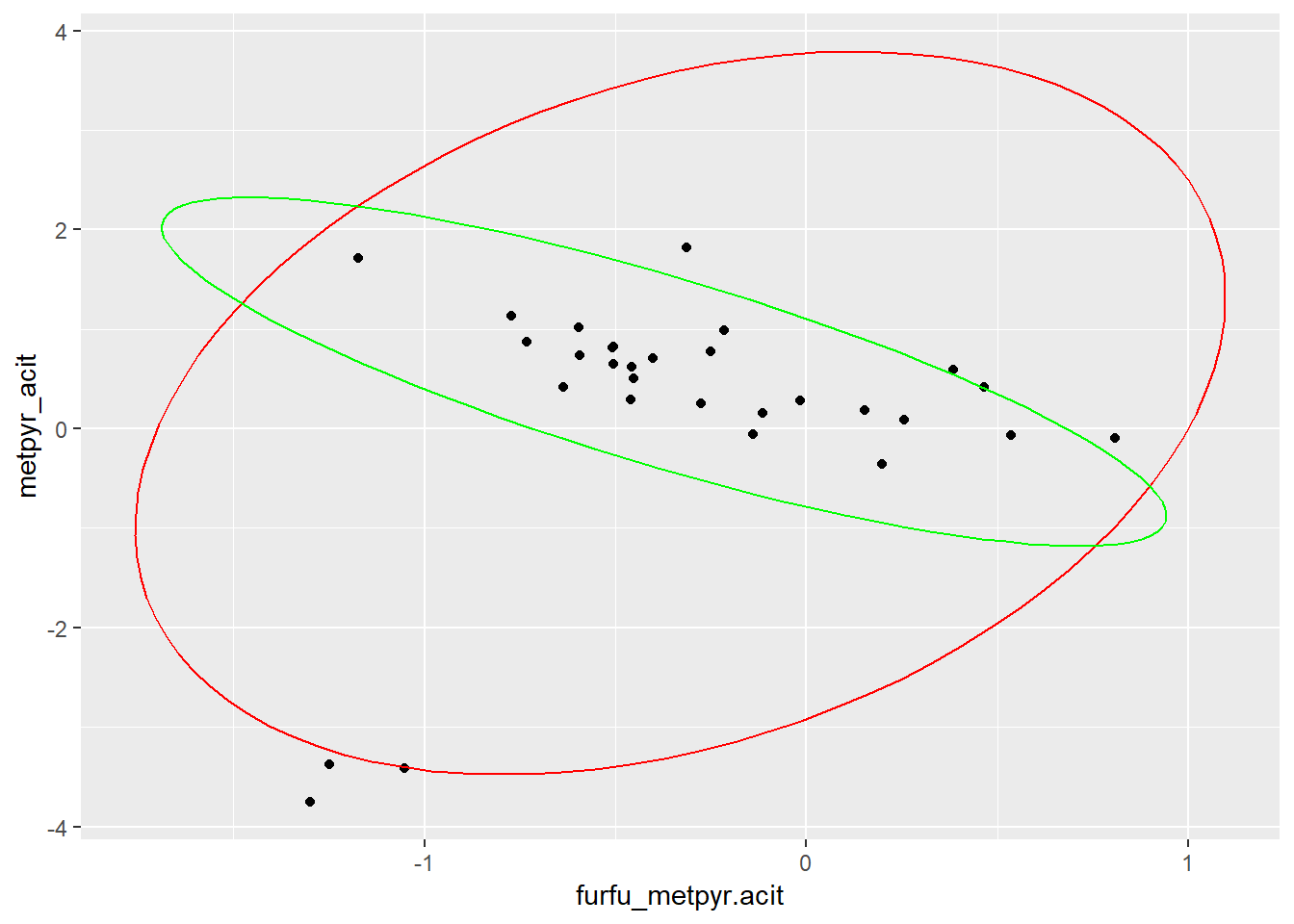
Figure 2.3: Valeurs manquantes sans (rouge) et avec (vert) méthodes robustes.
Les fonctions mvoutlier::sign1() et mvoutlier::sign2() utilise justement les méthodes robustes pour détecter des valeurs aberrantes. La méthode mvoutlier::sign1() sebase sur les composantes principales robustes.
coffee_ilr <- coffee_ilr %>%
mutate(is_outlier = sign2(as.matrix(.), qcrit = 0.975)$wfinal01 == 0)
coffee_ilr %>%
ggplot(mapping = aes(x = furfu_metpyr.acit, y = metpyr_acit)) +
geom_point(mapping = aes(colour = is_outlier)) +
geom_path(data = elldev_ilr, aes(x = furfu_metpyr.acit, y = metpyr_acit), colour = "red") +
geom_path(data = elldev_ilr_rob, aes(x = furfu_metpyr.acit, y = metpyr_acit), colour = "green")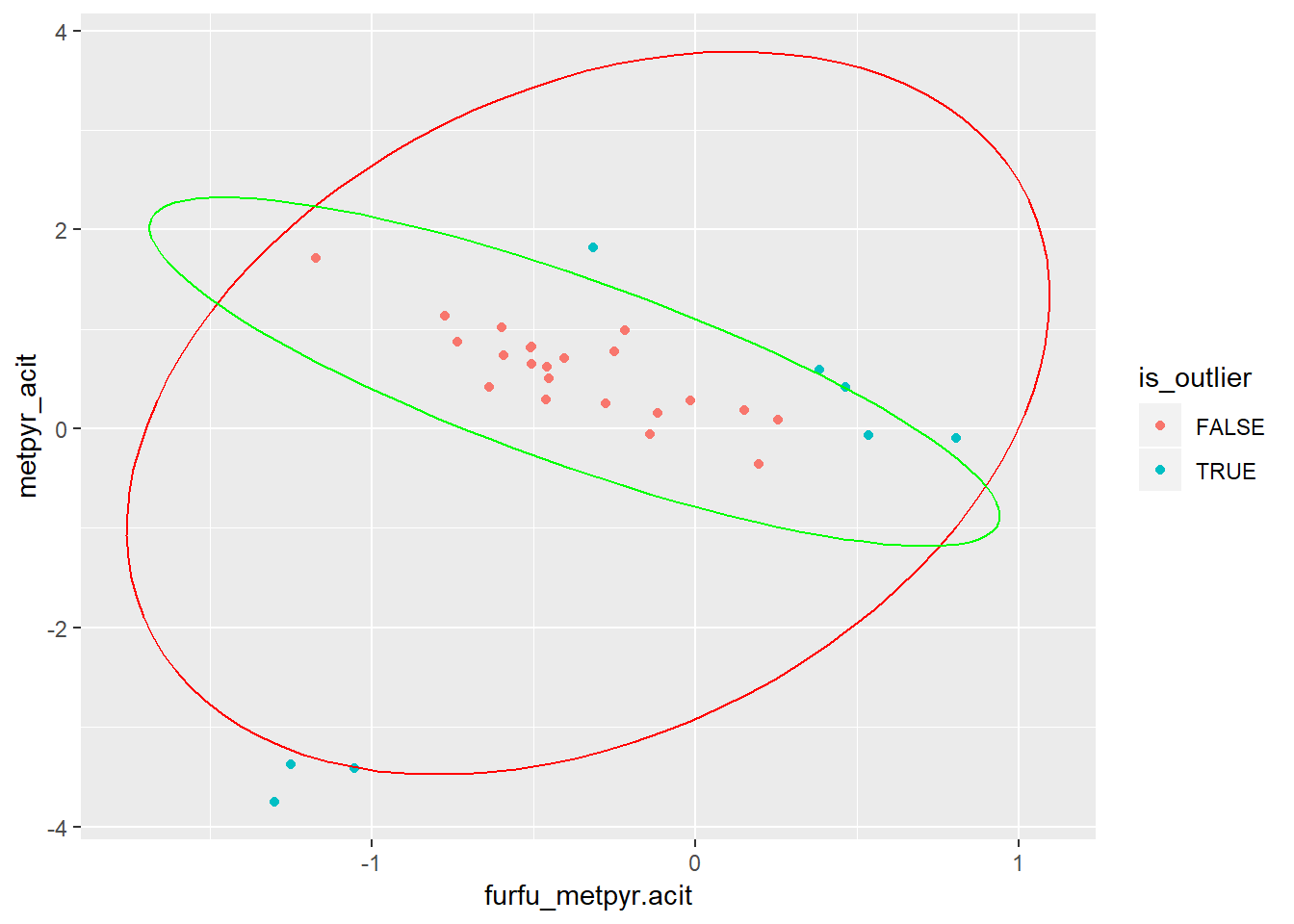
Figure 2.4: Valeurs manquantes sans (rouge) et avec (vert) méthodes robustes.
2.3 Biostats compositionnelles
La régression linéaire est une des méthodes statistiques les plus communes. Elle permet d’apprécier les effets de variables explicatives sur des variables-réponse. À cet égard, les compositions peuvent autant expliquer que servir de variable de sortie.
2.3.1 Les compositions comme variables-réponse
Les données ArcticLake présentent la granulo pour différentes profondeurs de sédiments. La profondeur peut-être expliquer la granulo? Nous allons d’abord transformer la texture en ilr.
data("ArcticLake")
granu_comp <- acomp(ArcticLake[, -4])
sbp <- matrix(c(1, 1,-1,
1,-1, 0),
ncol = 3,
byrow = TRUE)
granu_ilr <- ilr(granu_comp, V = gsi.buildilrBase(t(sbp))) %>% as_tibble() %>%
mutate(depth = ArcticLake[, 4])
names(granu_ilr)[1:2] <- c("c_sS", "s_S")Nous avons ici deux sorties (balances [c | s,S] et [s | S]) et une entrée (la profondeur). Créons deux modèles.
mod1 <- lm(c_sS ~ depth, granu_ilr)
mod2 <- lm(s_S ~ depth, granu_ilr)Inspectons le modèle 1.
summary(mod1)##
## Call:
## lm(formula = c_sS ~ depth, data = granu_ilr)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.52419 -0.51847 -0.04614 0.46839 2.52374
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.86983 0.26341 7.099 2.09e-08 ***
## depth -0.03545 0.00475 -7.464 6.88e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.822 on 37 degrees of freedom
## Multiple R-squared: 0.6009, Adjusted R-squared: 0.5901
## F-statistic: 55.72 on 1 and 37 DF, p-value: 6.882e-09L’intercept est la valeur de la balance [c | s,S] à profondeur nulle. Une balance positive montre que l’argile prend moins de place dans la composition que la moyenne géométrique du limon et du sable. La pente négative montre que la balance tend à diminuer en profondeur, c’est à dire que l’argile prend relativement de plus en plus de place en profondeur.
Prédisons nos ilr.
pred1 <- predict(mod1)
pred2 <- predict(mod2)
par(mfrow = c(1, 2))
plot(granu_ilr$c_sS, -granu_ilr$depth)
lines(pred1, -granu_ilr$depth, col = "red")
plot(granu_ilr$s_S, -granu_ilr$depth)
lines(pred2, -granu_ilr$depth, col = "red")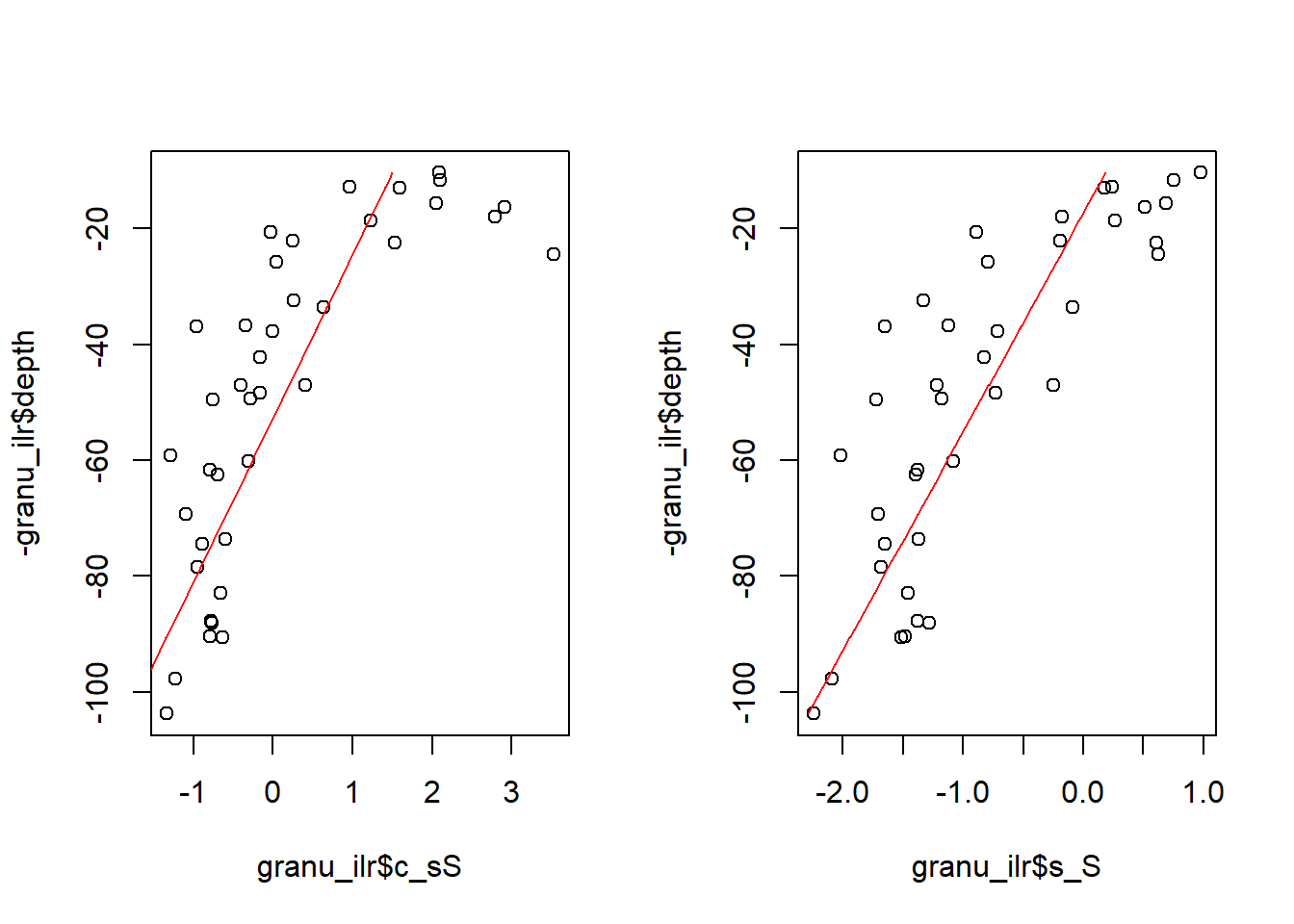
Les modèles linéaires ne sont vraisemblabelment pas adéquats: on aurait avantage à transformer la profondeur en log. Mais passons. Le fait est que l’on peut transformer nos deux prédictions en composition, puis présenter une régression linéaire dans un diagramme ternaire.
pred_comp <- ilrInv(cbind(pred1, pred2), V = gsi.buildilrBase(t(sbp)))
plot(granu_comp)
lines(pred_comp, col = "red")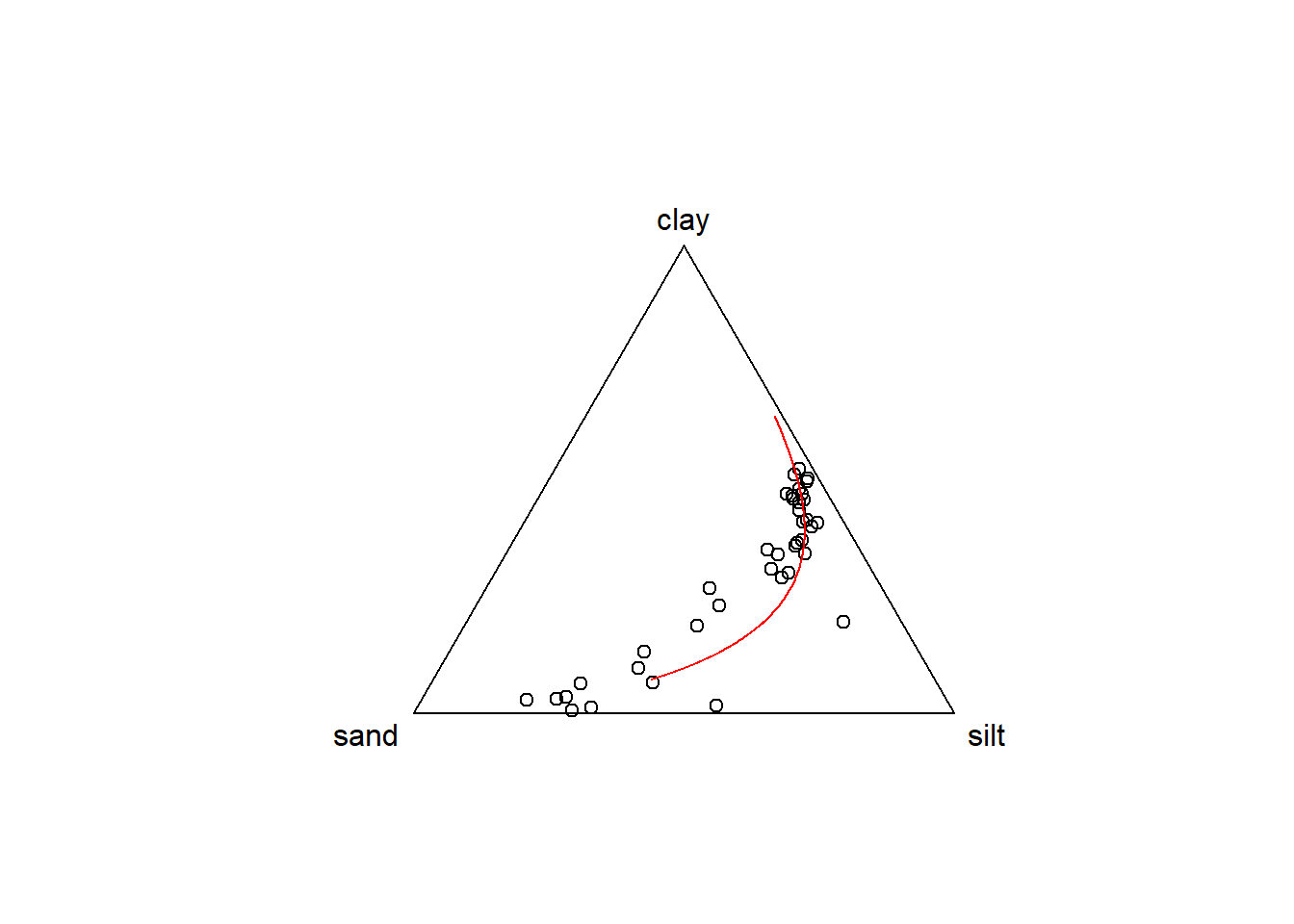
2.3.2 Les compositions comme variables explicatives
Disons que j’aimerais voir quel est l’effet de la compostion chimique d’un humus sur son pH.
data("humus")
humus_comp <- humus %>%
dplyr::select(C, N, P, K, Ca, Mg) %>%
mutate(Fv = 1e6 - C - N - P - K - Ca - Mg) %>%
acomp(.)
sbp <- matrix(c( 1, 1, 1, 1, 1, 1,-1,
-1, 1, 1, 1, 1, 1, 0,
0, 1, 1,-1,-1,-1, 0,
0, 1,-1, 0, 0, 0, 0,
0, 0, 0, 1,-1,-1, 0,
0, 0, 0, 0, 1,-1, 0),
byrow = TRUE, ncol = 7)
CoDaDendrogram(humus_comp, V = gsi.buildilrBase(t(sbp)))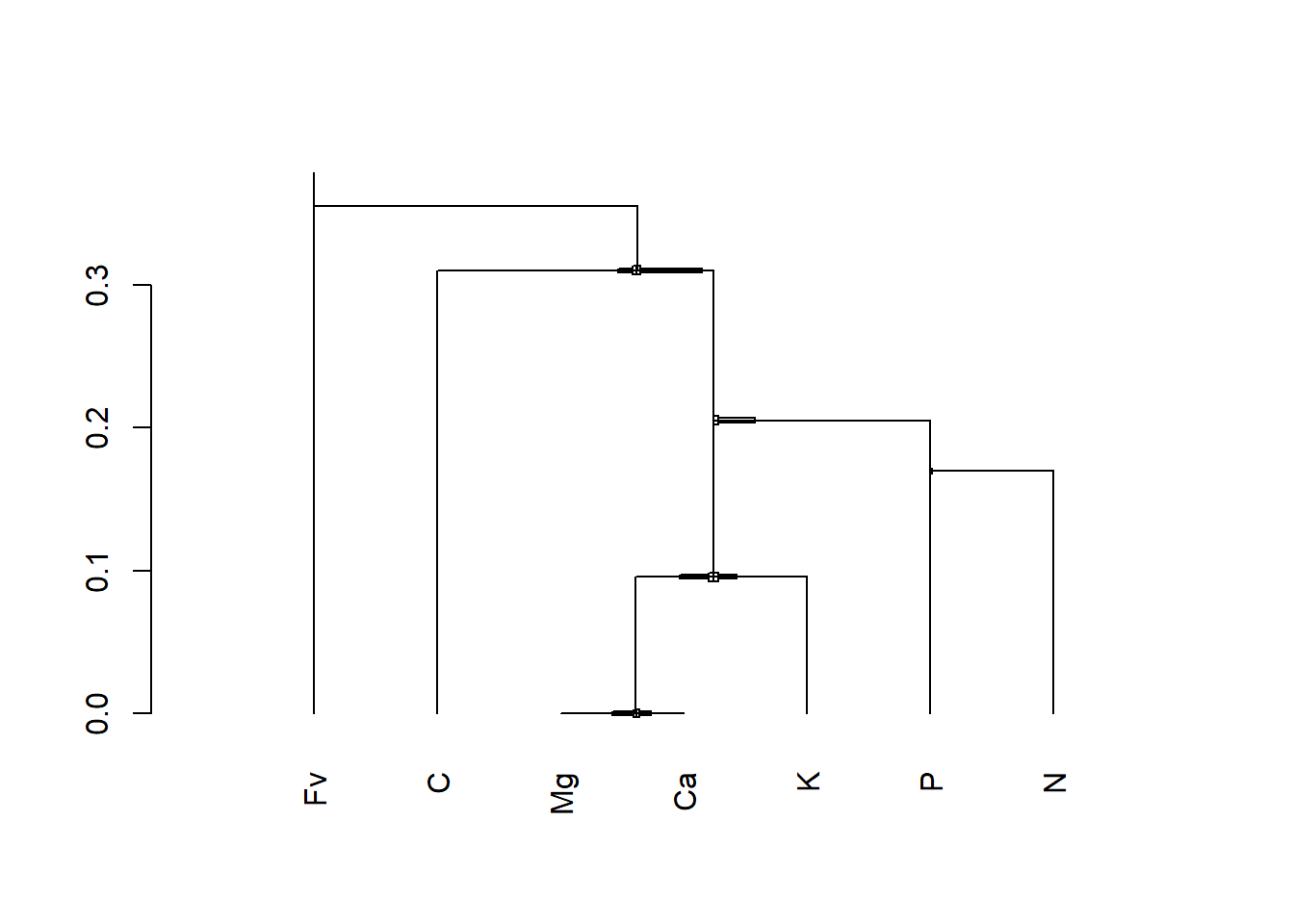
La SBP est structurée pour exclure d’abord l’amalgamation Fv dans la balance [Fv | C,Mg,Ca,K,P,N]. Puis, J’exclue le carbone des nutriments dans [C | Mg,Ca,K,P,N]. La balance suivante, [Mg,Ca,K | P,N], est un log-ratio entre anions et cations. Ensuite, le Redfield-ratio est exprimé par la balance [P | N]. Puis je balance les cations selon leur valence dans [Mg,Ca | K]. La balance restante est [Mg | Ca].
Calculons les ilr puis lançons le modèle linéaire.
humus_ilr <- ilr(humus_comp, V = gsi.buildilrBase(t(sbp))) %>%
as_tibble()J’ai conçu un petit algorithme pour définit les balances. Pour l’utiliser, il faut exécuter son code et il faut que la SBP ait des noms de colonne.
source("https://raw.githubusercontent.com/essicolo/AgFun/master/ilrDefinition.R")
colnames(sbp) <- colnames(humus_comp)
names(humus_ilr) <- ilrDefinition(sbp, "-+")J’ajoute la colonne pH au tableau d’ilr, puis je lance le modèle linéaire.
humus_ilr <- humus_ilr %>%
mutate(pH = humus$pH)
modlin <- lm(pH ~ ., humus_ilr)
summary(modlin)##
## Call:
## lm(formula = pH ~ ., data = humus_ilr)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.75228 -0.11364 -0.01487 0.10291 0.79732
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.21737 0.58342 7.229 1.46e-12 ***
## `[Fv | Mg,Ca,K,P,N,C]` 0.11781 0.06061 1.944 0.0524 .
## `[C | Mg,Ca,K,P,N]` 0.80107 0.05695 14.065 < 2e-16 ***
## `[Mg,Ca,K | P,N]` 0.15985 0.03066 5.213 2.55e-07 ***
## `[P | N]` 0.07187 0.05405 1.330 0.1841
## `[Mg,Ca | K]` -0.19108 0.02628 -7.271 1.10e-12 ***
## `[Mg | Ca]` 0.02883 0.02570 1.122 0.2624
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1806 on 610 degrees of freedom
## Multiple R-squared: 0.4846, Adjusted R-squared: 0.4795
## F-statistic: 95.59 on 6 and 610 DF, p-value: < 2.2e-16L’intercept est la valeur du pH lorsque toutes les balances sont nulles. Cette information n’est pas intéressante. Quant aux pentes, on pourra les interpréter comme suit. Une pente positive de {r} round(coef(modlin)[3], 5) sur la variable [C | Mg,Ca,K,P,N] signifie que plus la balance est élevée, plus le pH est élevé. Une balance plus élevée signifie que la moyenne géométrique du numérateur [Mg,Ca,K,P,N] gagne de plus en plus en importance par rapport que celle du dénominateur [C].
De même, une pente de {r} round(coef(modlin)[6], 5) indique qu’à chaque fois que la balance [Mg,Ca | K] augmente de 1 unité (c’est ce qui se passerait si K augmenterait ou que Mg et/ou Ca diminuerait), le pH diminue de {r} round(coef(modlin)[6], 5).
Les coefficients de pente, qui sont des perspectives exprimées en balances, changeraient si la sbp était différente, mais la régression serait la même (même intercept, même R²). On pourra même transformer les pente en une composition pour obtenir ce que l’on appelle une perturbation (Filzmoser et al. (2018), chapitre 3.2).
ilrInv(coef(modlin)[-1], V = gsi.buildilrBase(t(sbp)))## C N P K Ca Mg
## 0.06696377 0.18494427 0.16706972 0.12996935 0.16762141 0.16092365
## Fv
## 0.12250782
## attr(,"class")
## [1] acomp2.4 Bioheuristique compositionnelle
2.4.1 Partitionnement
La distance entre deux compositions est un distance d’Aitchison. Cette distance est une distance euclidienne calculée sur des clr ou des ilr. Les distances n’étant pas affectées pas la formulation de la sbp, je me permets d’utiliser une sbp quelconque.
coffee_ilr2 <- coffee %>%
dplyr::select(-sort) %>%
ilr(.) %>%
as_tibble()
coffee_aitdist <- coffee_ilr2 %>%
dist(., method = "euclidian")La distance permet notamment d’effectuer du partitionnement (clustering, je vous réfère aux notes de mon cours GAE-7007 pour plus de détails sur le partitionnement).
coffee_clust <- as.dendrogram(hclust(coffee_aitdist, method = "average"))
library("dendextend") # pour colorer les feuilles
labels_colors(coffee_clust) <- as.numeric(coffee$sort)
plot(coffee_clust)
Les échantillons 6 et 15 semblent mal classés, mais somme toute, c’est pas mal!
2.4.2 La distance d’Aitchison par rapport au barycentre est une diversité
Notez que la distance d’Aitchison par rapport au barycentre d’une composition (où toutes les proportions sont égales) est un indicateur de diversité.
Je créé une grille sur laquelle je vais calculer des indicateurs de diversité.
n <- 10000
p1 <- runif(n, min=0, max=1)
p2 <- runif(n, min=0, max=1)
p3 <- runif(n, min=0, max=1)
comp_grid <- tibble(p1, p2, p3)
ilr_grid <- ilr(comp_grid)Puis je calcule la distance d’Aitchison par rapport au barycentre.
library("vegan")
ilr_grid <- ilr(comp_grid)
comp_grid <- comp_grid %>%
mutate(aitdist = sqrt(ilr_grid[, 1]^2 + ilr_grid[, 2]^2),
shannon = diversity(., index = "shannon"))Les graphiques sont crées ici avec ggtern.
library("ggtern")
gg_aitdist <- ggtern(data = comp_grid, aes(p1, p2, p3)) +
geom_point(aes(colour = aitdist)) +
scale_colour_viridis_c(option = "inferno", direction = 1)
gg_shannon <- ggtern(data = comp_grid, aes(p1, p2, p3)) +
geom_point(aes(colour = shannon)) +
scale_colour_viridis_c(option = "inferno", direction = -1)
cowplot::plot_grid(gg_aitdist, gg_shannon)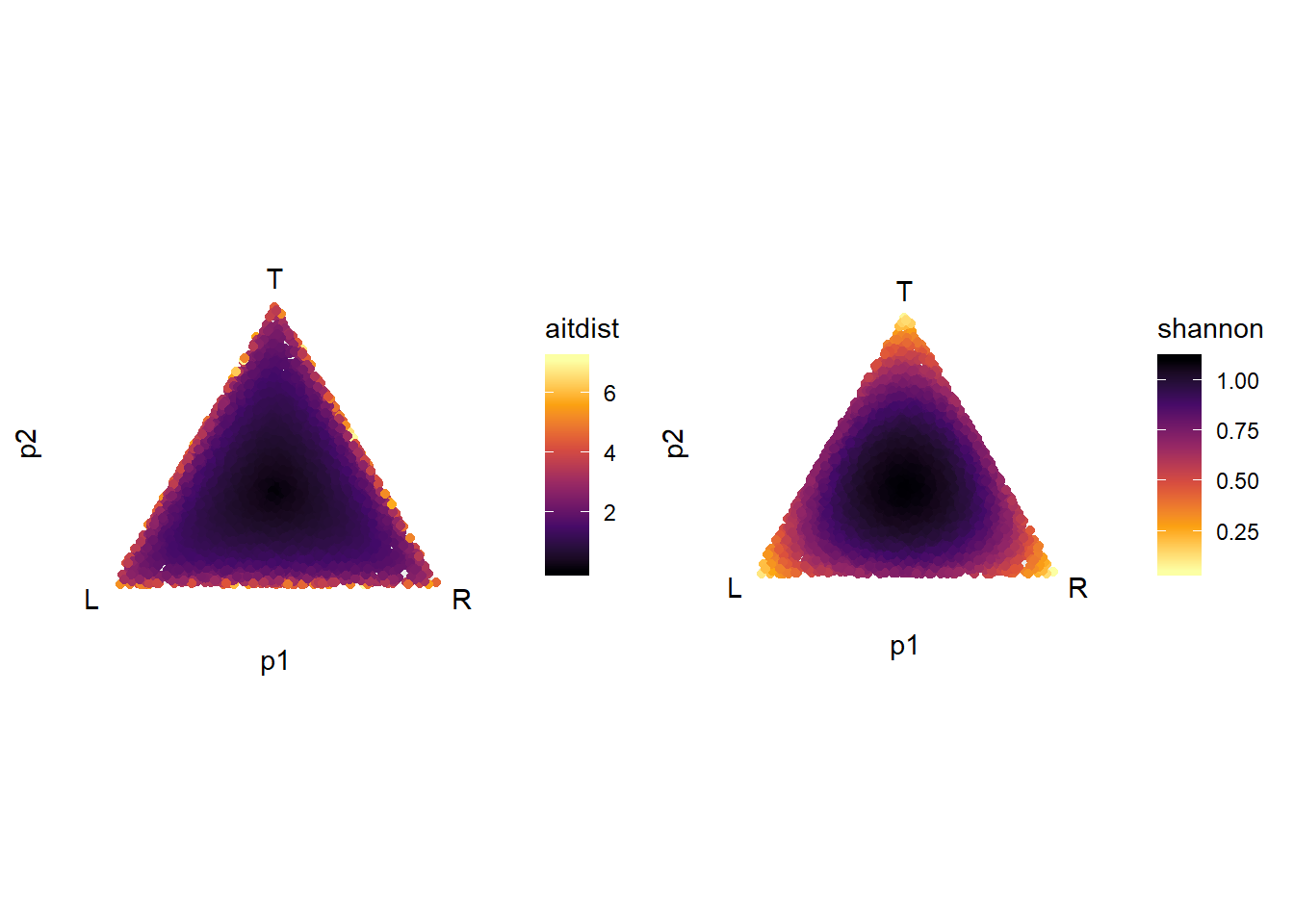
2.4.3 Ordination
Exercice d’analyse discriminante sur l’ionome.